反编译器后端 - 结构分析

结构分析负责将IR转换为伪C代码。

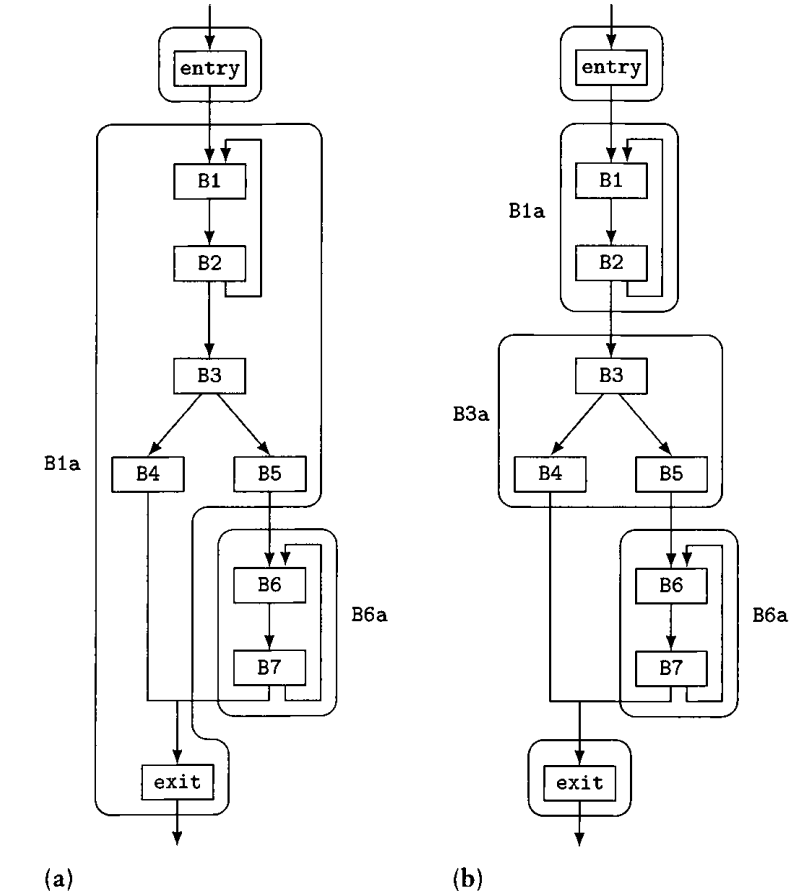
使用Goto语句的IR转C

• 给所有的基本块前添加标号，对于任意控制流跳转，使用goto实现。最后删除无用的标号。

这种方法可以考虑作为现有算法的辅助，将算法无法处理的边转换为Goto语句。算法可以自由选择能够折叠的边进行折叠，从而只需要考虑实际的结构分析效果，不必纠结算法的完善和鲁棒性。

Structural Analysis 和 Reducible Control Flow

• PPT(结尾介绍了Reducibility)
• PPT(介绍了Reducibility编译原理相关的内容)
• PPT:介绍了structural analysis 特别说明了
• PPT:更详细地介绍了structural analysis
• 介绍了T1 T2转换

一个CFG如果是Reducible的，则我们可以将图上所有边分割为两部分，前向边，和反向边

• 前向边构成有向无环图，每个节点可以从entry到达。
• 反向边的目标节点都支配源节点。

定义2：T1 T2转换 一个CFG如果是reducible的，可以通过规则将图中的节点递归缩减为单个节点。

• T1 自环可以被缩减
• T2 如果某个节点仅有一个前驱，则可以将该节点缩入这个前驱节点

然而，有个PPT里面说，这种T1 T2转换，对控制流的缩减，从而对控制流划分的层次结构，不一定规范地符合真实源码里面的划分。T1 T2转换是最早的，最简单的一种interval analysis.

Structural Analysis For Dataflow Analysis

相关资料

• 《A Structural Algorithm for Decompilation》反编译的结构分析
  • 在一个CMU的lecture notes里面提到了这个paper
• 《Advanced Compiler Design and Implementation》 非常经典的编译器理论书籍
  • Phoenix论文里，提到结构分析的时候，也推荐了让读者去看这里。因此非常值得读一读。
  • 在203页更详细地介绍了structural analysis。建议从196页的Reducibility开始阅读。（书里面的页码，不是pdf的页码）这些结构分析都比较老了，而且有的不太是为反编译设计的。

概述：在编译优化方面，有研究人员提出，要是在IR（CFG）层面能够用上AST层面的信息（IF，While，For控制流结构），能够加速现有的数据流分析。然而在IR（CFG）层面，高级语言的结构信息已经丢失了。因此，有部分研究人员提出了通过模式匹配的方式，从CFG中识别出控制流结构。由此诞生了interval analysis算法，后续发展出了Structural Analysis。

结构分析一般可以分为一下几个步骤：

1. 类似interval analysis的嵌套区域划分。
2. 将划分好的子区域进行模式匹配，匹配为高级语言的控制结构。

定义：(Maximal Interval)：最大的，单入口子图，（假设入口节点为I）且子图中所有闭合的路径都包含I。

定义：Minimal Interval：是指：(1) 一个natural loop，(2)一个最大的有向无环子图，(3)一个最小的不可规约区域。和maximal interval主要区别大概在于，maximal interval划分loop的时候会把连带的有向无环分支带上，而minimal interval会单独分出来。

一个minimal interval和maximal interval的区别如下：左边是maximal interval的划分，右边是minimal interval的划分。

定义：Natural Loop 背景：在编译原理里面的loop，也是希望仅有单个节点支配整个loop。我们使用支配关系寻找loop的时候，由于它是一个loop，因此必然至少有个“反向边”，不然构不成一个环。 Natural Loop的关键在于那个反向边，即头节点支配尾节点的边。

一个反向边的Natural Loop（即，natural loop严格说并不是一个单独的概念，反而是对一条反向边而言的。），是指，最小的，包括反向边头和尾节点的节点集合，集合内所有节点的前驱，要么在集合内，要么这个节点是entry节点，前驱是entry的前驱。

当你移除那个entry节点的时候，因为entry节点支配其他节点，图就被分裂成了两部分。此时寻找所有有路径到达t的节点（t这里指反向边的源节点），这些节点和entry节点构成了natural loop。

在《A Structural Algorithm for Decompilation》里直接使用了类似T1-T2规约的方式划分interval。

Interval Analysis (maximal interval)：该算法就是《A Structural Algorithm for Decompilation》里面用的，算法如下：

迭代性：该算法是一个迭代的算法，每一次迭代找出节点集合后，即使可以看作一个新的单个抽象节点，也不会产生新的节点集合包含这些本轮生成的抽象节点了，这些Interval嵌套的情况是由下一轮迭代负责的。（图片里的算法不包含这个迭代，迭代在另外一个没截图的算法里）

步骤：

• 从entry节点开始，依次类似T1 T2规约的方法（即，“看是否某节点仅有一个前驱”的拓展版，看某节点的前驱是否都在集合里）把节点加入集合中。如果结束了，就从当前集合的后继节点里抓节点出来再进行这个过程。直到所有节点都被归入了某个集合。
• 更新H的那一行代码的意思是：加入H的新节点，(1)不属于当前规约好的集合，(2)直接前驱在当前规约好的集合里。 （即，按顺序弄。）

在《Advanced Compiler Design and Implementation》里提到这种方式划分的是Maximal Interval。书中还提出了改进版的算法，划分的是Minimal Interval，划分效果更好，更小的区域便于后续划分高级语言的控制结构。

Interval Analysis (minimal interval)：该算法是《Advanced Compiler Design and Implementation》提出的改进版。它将CFG划分为三个部分，无环（acylic），natural loop和improper region。无环部分即有向无环子图，其他两种区域则包含环。

• proper region和improper region：proper region指一些虽然无环，但是也不能被简单的if-else等结构匹配的无环部分。improper region与之对应，有环，但是是比较复杂的环。

步骤：

1. 使用一个后序遍历找到loop header，和improper region的header。（后面再详细解释）
2. 对每个loop header构建natural loop区域。(使用支配图，判断是否有前驱节点指过来的边是反向边，即head dom tail)
3. 对improper region的header构建minimal SCC。（即只把环分离出来）
   1. 构建区域之后，对（区域的）所有的直接后继节点构建最大的有向无环子图（把环上长出的分支分离出来），如果成功弄出节点数量大于1的子图，就构建一个有向无环区域。
4. 递归整个过程直到终止。

可以感受到，这其实是基于前一个算法，融合了把有向无环的子区域分离的想法。同时还顺便分离了有环区域中的natural loop。（但是，有一些具体的实现细节也还是不清楚。。）下面详细解释算法细节。

背景1 深度优先遍历与逆后序遍历： Depth First Spanning Tree 是在DFS遍历过程中生成的一个树。基本思想是，DFS遍历过程中，会出现一种情况：判断当前节点指向其他节点的一条边的时候，发现这个边指向的目标节点已经被访问过了，所以就不需要沿着这条边过去了。因此可以将边划分为遍历使用了的边，和遍历过程中没有使用的边。

在深度优先遍历时，怎么才算是反向边？当然是这条边指向了已经被访问的节点。即遍历时发现指向的地方已经访问过了。这个过程并不是确定性的：即，也有可能出现，根据选择的子节点不同导致反向边不同的情况。比如两个子树交叉指向隔壁子树的更高的节点。深度优先遍历的时候，走过的边属于前向边（forward）。如果某条边反过来就属于前向边，则它是反向边（和某个前向边形成2节点的小环）。剩下的边属于交叉边。

是否完全确定反向边？：在《A Structural Algorithm for Decompilation》里直接使用了类似T1-T2规约的方式划分interval。后面判断是否是loop的时候提到，只需要检查interval的header的前驱指过来的边是不是反向边。而且只需要看后序遍历的顺序上的关系即可。我们这里探讨的问题是：**（检查interval header的predecessor）真的只需要看后续遍历的顺序就可以确定是否是反向边吗？**反向边的定义是，head节点支配tail节点。假如我们有个interval，有个back edge，如果想破坏这个支配关系的同时，保留后序遍历的顺序。假如根节点在DFS优先遍历左子树，我们的interval也在左子树，我们从右子树引一条边过来，这样不会影响左子树节点在后序遍历的顺序。同时我们把边指向header到tail节点的路径上，这样head就不再支配tail了。这样不就破坏了这个关系了吗？除非，这样引入的边会破坏interval的划分。确实，我们考虑那个被指向的节点，这个节点之前之所以会被归到这个interval，是因为它的所有前驱都在interval里了。这样增加的边会影响interval的划分，因此我们没能找到反例。

结构分析算法(《Advanced Compiler Design and Implementation》) 这边书中的算法是基于最早的结构分析《Structural Analysis: A New Approach to Flow Analysis in Optimizing Compilers》的改进。它的区域类型有：Block, IfThen, IfThenElse, Case, Proper, SelfLoop, WhileLoop, NaturalLoop, Improper这几种。

算法的大体结构如下：（书中205页）

1. 使用一个DFS_Postorder算法，给每个节点标上序号。
2. 在一系列的节点遍历中，不断辨识出新的区域，把这些区域规约成单个抽象节点（因此可能需要修复图结构，并且可能需要重新做后序遍历）。
   1. 规约时，把进入区域的边，离开区域的边作为这个抽象节点和其他节点的边。
3. 直到最后规约为仅一个节点。

Structural Analysis For Decompilation

概述：

然而，上面介绍的，为数据流分析加速设计的结构分析，用于反编译有着根本性的缺点。

1. 仅识别了一些简单的图模式。虽然通过递归，能够识别这些模式的组合，但当出现了复杂的图的时候，会完全放弃识别。无环图被识别为Proper Region，有环图被识别为Improper Region。
   1. 这对数据流分析算法没有影响，因为没识别出来可以按照旧的方式分析，只不过无法加速了。然而，这一点对我们反编译非常致命，直接放弃了划分。
      1. Phoenix在usenix 2013提出了，可以将部分边转成goto，从而能够继续识别出更多的控制流结构。
2. 本质上，稍微复杂一点的CFG，确实就不能识别控制流结构了。

SESS

**Single entry single successor (SESS)**分析

来自《Enhanced Structural Analysis for C Code Reconstruction from IR Code》论文中的3.3节。（论文中3.1、3.2回顾了一下什么是结构分析）。

背景：结构分析其实没有考虑break，continue等跳转指令。带有这些跳出语句的，也可能被归类为proper/improper region。

定义：假设有一个CFG，内部划分了SESS区域R，唯一的entry节点是r，successor节点是s，则有以下性质：

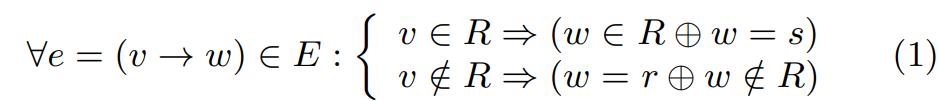
SESS区域：entry r属于region，successor s不属于区域内（看作区域的线性后继块）。

• 对于（整个图的）任意边，如果source属于区域内
  • 要么target属于区域内，区域内部边
  • 要么target等于successor节点
• 如果source不属于区域内
  • 要么target是entry节点（进入）
  • 要么target不属于区域内（区域外部边）

有哪些边被否认了？区域内部到区域外部的，不经过entry和exit的边。

Tail Region：文中提出了Tail Region的概念，它为现实中break的情况设计。一个带break语句的基本块，原本有一个很难处理的跳出的边。有了tail region之后，把它识别成tail region，就暂时假装没有那个边，继续做相关分析。

一些其他点：

• 论文中提到有这些性质的区域可以直接输出为C语言代码。因此SESS算法的目的是让SESS区域覆盖尽可能多的边。
• 在原有匹配cyclic region，acyclic region之后，如果匹配失败，就尝试匹配tail region。这里在Phoenix里面提到，这篇论文里没有写清楚具体的匹配算法。而且他们发现，经常确实也匹配不到这种tail region，如果图太复杂还是会失败。
• 关于论文没有说清楚的其他点，首先是怎么识别SESS region吧，可能是在原有的划分region基础上再做些判断。其次是怎么识别tail region的跳走的边。可能是识别region的基础上，看边是不是跳到head和tail的吧。

Interval Analysis as a pre-step?：上面介绍时，似乎说Interval分析是结构分析的预处理步骤。Interval分析可以划分子图，然后子图再去模式匹配。然而观察到，论文里给出的算法居然看不出来有做Interval Analysis。也没有写清楚如何判断一个节点后面的区域是cyclic的，还是acyclic的。这是为什么？

• Acyclic Region：识别是否是IF的三角形，IF-ELSE的菱形。如果不是，就返回匹配失败（归类为proper region）。
• Cyclic Region：识别natural loop。如果无法识别，还是返回失败(归类为improper region)。

可以发现，如果匹配失败，总要用fallback去删边，所以详尽地划分cyclic，acyclic interval也没有意义了，反而是给自己增加了限制，限制必须在这个interval区域内匹配。我们只需要直接匹配过去便是，不必太在于具体是什么region。

natural loop，如果才能

子问题：有向无环图的规约

• 必然存在“叶子节点”，即不指向其他节点的节点。根据这种节点的被指向情况分类
  • 仅有一个节点指向它：类似叶子节点，可以规约成block。
  • 有多个节点指向它：后续寻找菱形，三角形，多分叉合并继续规约。 然而，对于任意子图，并不是都一定能规约成IF-ELSE结构，比如下面的图：

Phoenix 第一个“真正实用”的结构恢复算法

• [Phoenix] 《Native x86 Decompilation Using Semantics-Preserving Structural Analysis and Iterative Control-Flow Structuring》 slides
• reko的实现

paper的3.1节介绍了算法框架，和结构分析很相似。

• 使用后序遍历，遍历每个节点。直观上子节点被处理合并后再处理父节点。遍历每个节点时，判断是acyclic还是cyclic的。
  • 如果是acyclic的区域，算法尝试匹配几种简单的模式，以及潜在的switch语句。匹配不了还是会跳过
  • 如果是cyclic的区域，算法尝试找natural loop，匹配常见的循环模式，或者就是普通的loop。实在处理不了还是跳过
    • 如果匹配失败，进入Loop Refinement阶段（3.6节）。
  • 如果一轮下来都匹配失败了，则使用“最后手段”将一个跳转归类为goto，并忽视它，再重新进行一轮。
    • 优先选择：源节点没有支配目标节点。源节点支配了目标节点的边，大概率是比较重要的边。
    • 优先选择：目标节点支配了源节点。这种不就是natural loop的边吗？

具体应该选择哪些边移除？当前的选择到底好不好？确实是一个值得思考的问题。

Loop的节点：

• 原始的定义：一个反向边的Natural Loop（即，natural loop严格说并不是一个单独的概念，反而是对一条反向边而言的。），是指，最小的，包括反向边头和尾节点的节点集合，集合内所有节点的前驱，要么在集合内，要么这个节点是entry节点，前驱是entry的前驱。
• 存在的问题：不能涵盖一些break语句所在基本块的节点。这些节点被上面定义的“最小”排除。
• 新的定义：除了原始定义中的节点，额外增加了一些节点。
  • 新增节点的定义1：被loop header, 即entry支配的节点中：排除从loop的successor节点，不经过loop header可达的节点。
  • 新增节点的定义2：满足两个条件：条件1：被entry支配。条件2，从loop的successor节点出发，不经过loop header的条件下，不可达。

reko的实现

• Region：算法的主体数据结构，对List<Statement>的封装，但是内部不止可以放指令，还可以放statement。当折叠If, While等结构的时候，它们作为单个statement。
  • 最开始的时候根据基本块的后继块数量情况，每个块创建region，同时将线性的指令都转换为statement。(reko - RegionGraphBuilder)，在算法的迭代下不断折叠。
  • 最后的效果就是整个函数体变成单个linear region。
• Statement：已经结构化的基本块/statement的集合。
  • 不使用Expression，而是结合LLVM的指令。
• LLVM语句序列化写出来就已经可以看作全是goto的高级语言了。因此不额外增加goto statement。

算法的输入输出：首先包括一个将LLVM指令重新折叠为C表达式的数据结构，负责创建所有其他语句。而结构恢复算法，则主要负责创建if，else，while，这些语句。我们基于Clang AST生成C/C++源码。可以发现，clang中有些源码分析也需要CFG，因此也为源码块的CFG数据结构。基于Clang内置的CFG数据结构，我们先将IR转换为这里的CFG结构，然后再由结构分析基于CFG生成完整的文件的AST。

结构化算法尝试将现有的基本块CFG的IR架构，重新组织为类似AST的形式

• 可能会有这种原始的想法：能不能把结果表示为CFG上的简单标记？似乎是不能的，因为是完全不一样的东西。
  • 比如，把结构嵌套折叠到了一个条件跳转里。但是这种折叠，在IR上不一定看得出来。比如，菱形的IF-Then-Else结构，单看IF块就没有明显的从if开头，到整个if结构的successor的边。如果仅把结构分析的结果看作是对边的标记，这里肯定是丢失了信息的。
• LLVM的SSA能否和AST共存？稍微搜了一下，不太能。而且在表达式折叠的时候，遇到这种跨基本块的phi数据流，也适合创建新的变量。

Dream

• Dream:《No More Gotos: Decompilation Using Pattern-Independent Control-Flow Structuring and Semantics-Preserving Transformations》 slides
• fcd decompiler and its blog posts (404 now, find content in web archive)
  • http://zneak.github.io/fcd/2016/02/24/seseloop.html
  • http://zneak.github.io/fcd/2016/02/17/structuring.html
  • http://zneak.github.io/fcd/2016/02/21/csaw-wyvern.html

实现

目标是支持任意IR的转C语言伪代码。一些IR层丢失的类型信息（整数是否有符号，结构体的字段名称等）需要额外的数据结构。

代码优化：Phi指令不好提供支持，我们使用demoteSSA去除Phi指令。为了消除demoteSSA带来的额外空基本块，我们再调用了SimplifyCFG pass。

表达式折叠

副作用的处理：不考虑是否有副作用，即都当有副作用处理。暂时不考虑无副作用的表达式为了简洁的折叠。例如int tmp = 1+2; f(tmp); g(tmp) 不会折叠为f(1+2); g(1+2);

• Stmt和Expr的划分：
  • 如果一个指令没有返回值，纯粹只有副作用，则作为Stmt。例如Store指令。
  • 如果一个指令可能有返回值，则作为Expr，根据引用情况和次数考虑
    • 如果指令没有使用者，则直接将表达式作为stmt插入。
    • 如果指令被基本块外指令引用，或者被当前基本块的指令引用多次，则创建局部变量，然后注册这个局部变量到ExprMap。
    • 如果指令被当前基本块内的指令引用，且仅被引用一次，则直接作为表达式折叠到对应的指令内。直接将当前表达式注册到ExprMap。

Expr现在的表示有bug。Call不好说作为expr还是stmt。并不是有副作用就应该作为Stmt。而是指令没有返回值，不会被作为value才作为Stmt。具体是否应该把Expr作为Stmt放下来，这个都得放。具体是否应该创建一个局部变量，得看是否在一个基本块。如果发现这个Expr的基本块和当前的基本块不同的话，就应该在那边为这个expr创建一个局部变量。

逻辑表达式: C/C++的and/or具有短路的性质。但在无副作用时这影响不大。但是在IR中，如果尝试直接优先折叠成and/or指令，则会不存在短路，语义发生变化。因此逻辑运算符需要在结构分析中处理。

• DemoteSSA会引入不必要的基本块，我们使用SimplifyCFG处理这些基本块。SimplifyCFG同时还会折叠and/or表达式，但是折叠后是select指令的形式。
  • select 指令对应ternary三元运算符。同时select 如果作用在i1，同时两边如果存在false或者true常量时，可以作为and/or处理。
    • select i1 expr1, i1 true, i1 expr2 -> expr1 || expr2
    • select i1 expr1, i1 expr2, i1 false -> expr1 && expr2
• LLVM里的instcombine会将这种模式转为and/or（见这里），但是我们不需要考虑那么多，直接两种都支持。

指令处理

类型

• 将IR类型对应地带着指针类型转换，冗余的解引用和取地址~~使用窥孔优化~~在生成AST时消除：IR的全局变量对应它的指针类型，alloca对应局部变量的指针类型。
  • 窥孔优化：clang没有自带的。根据ASTMatcher自己写一个吧。 根据这里，AST其实很难修改。
    • Clang::Tooling::transformer：将AST修改为对应的代码文本。通过再次parse，有可能可以实现类似AST修改的效果。
    • lib/Sema/TreeTransform.h内部库。没有细看。
    • clangTooling, rewriter: 例如这里, 在AST转文本代码的时候介入并进行修改。

名称

为了简化设计，全局不允许出现重名的情况。全局使用IdentifierInfo判断重名情况，重名时尝试增加"_1"递增的数字后缀。函数内使用Names判断重名情况

• 尽量还原LLVM IR，使用IR中的名称
  • GlobalVariable，Function等使用IR对应的名称。
  • 局部变量对应alloca指令，因此使用Alloca指令的名称。
  • 如果没有名称，则生成前缀加编号的临时名称，如func_1。

ConstantExpression

• 常量数组，常量结构体
  • 直接的对应是Compound literals再内置InitListExpr。但它会创建一个匿名对象，所以大部分情况还是不会转成它的。
    • 如果是在初始化变量，则直接转换成纯InitListExpr。
    • （暂未实现）如果在其他地方（如指令里）用到了，同时是递归的最外层，则
      • 结构体转换成ImplicitCastExpr(LValueToRValue) + Compound Literal + InitListExpr。
      • 数组转换成ImplicitCastExpr(ArrayToPointerDecay) + CompoundLiteralExpr(array) + InitListExpr。
    • 如果是递归创建内部的表达式，则只创建InitListExpr部分。
  • 如果遇到了ConstantInitializerZero，则应该转换为InitListExpr + array_filler: ImplicitValueInitExpr
  • 创建常量需要传入一个额外的类型：
    • 创建ImplicitValueInitExpr需要设置类型。
    • 创建Compound Literal也需要类型。
• 结构体类型
  • LLVM中预定义的结构体类型，提前遍历并存放好。维护一个从llvm type到RecordDecl的映射。
  • LLVM中的Literal 结构体转换为C语言中的匿名结构体。
    • 首先看当前llvm Type是否被映射和缓存，即该匿名结构体已经遇到过。
    • 直接创建一个匿名RecordDecl，加入映射，并直接插入到TranslationUnitDecl里的当前位置。
  • 结构体成员名字无法保存在IR中。（TODO，目前直接按顺序生成一个名字）
    • 结构体的成员名字可以考虑保存在Meta data，如DebugInfo里
    • 缺点：必须依附于这个类型的全局变量。不能直接依附到类型上。MataData只能依附于指令，函数等

BinaryOperator

• 加法：nsw，nuw。当溢出时会变成poison value。这个暂时不考虑。
• 移位运算：逻辑移位对应C语言无符号数字的移位，算数移位对应有符号数字的移位。（根据这里）

运算符优先级：Operator Precedence

C Operator Precedence

总体的优先级顺序：变量成员和数组访问和后缀一元运算符，前缀一元运算符，其他二元运算符。注意：

• 变量成员和数组访问其实可以看作是一种后缀一元运算符。Clang里这两者是单独的表达式类型。既然它们优先级最高，就不需要单独考虑处理。函数调用，强制类型转换同理。
• 一元运算符根据前缀和后缀分两个优先级。
• 三元运算符，中间可以看作已经带了括号，从而看作一个二元运算符。

增加函数考虑是否增加括号：

• 函数1：获取表达式优先级
  • 判断是一元，二元，三元，然后给出优先级数字值。
• 函数2：根据优先级获取结合律，返回bool类型，是左结合还是右结合
• 函数3：参数1 当前运算符优先级，参数2 子表达式优先级，参数3: bool is_left 运算符左边还是右边
  • 判断子表达式优先级是否低于当前一元运算符优先级，是则增加括号。
  • 如果优先级同级，调用函数2获取结合律信息，然后根据左结合和右结合处理。左结合运算符：如果同级则不需要在左边子表达式增加括号。
    • 如果结合率和当前处理的边相同则不需要括号，反之需要括号。

CallInst

• Organize and maintain a map from llvm functions to Clang function declarations.
• Handle function pointers: TODO

Alloca指令

根据alloca指令是否在函数开头的必经之路（从entry遍历找到只有一个succ和pred的集合）上，将alloca分为动态alloca和静态alloca。

• 静态Alloca：创建对应类型的变量。

• 动态Alloca（很少）：TODO，转换为alloca函数调用

• AllocaInst:

  • If the inst is at the outermost level, then create a corresponding local variable.
  • If not, this is a rare case, create corresponding calls to the alloca function.

GetElementPtr

LLVM数组与C数组的对应：

• C数组变量 -> LLVM数组指针再解引用一下（LLVM常通过指针操作变量）
• gep操作时第一个index不为0 -> C里面int arr[3]; (&arr) + 1 （意味着GEP不需要在开头默认解引用一下）
• gep如果有且只有第一个index，则类型不变 -> GEP结束隐含了取地址操作。

GEP中途每一步结束并没有保证结果是指针类型，而是在结束的时候额外做了取地址。 GEP每一步类型必定会细化：如果是指针，则会解引用（数组取成员0），如果是数组或者结构体，会取成员。

C的指针相关运算内部细节：

• 结构体运算：结构体值 -> 结构体成员值
  • 箭头运算：结构体指针 -> 结构体成员值 （在开始前先解引用）（对应Gep里的两步）
• 数组运算：
  • 数组值到数组成员值
  • 指针的数组运算（不考虑）：指针到指针解引用后成员值（指针运算外加解引用）（对应Gep里的两步）
    • 解引用运算 = 数组下标取0
• 指针加减法运算：指针值 -> 新指针值
• 解引用运算 + 取地址
  • 指针 -> 指针内部成员指针

GetElementPtr先获取内部指针值的类型，然后依次处理每个下标：

• 如果是结构体成员或者数组，则先解引用，然后增加运算，然后再取地址。

添加注释

添加注释不是简单地插入AST，因为Clang没有把注释这样管理，而是直接插入到ASTContext里面，而且要创建RawComment，而不是对应的语法树结构。没有找到将对应的Comment类插入进去的函数，应该需要自己实现。可能需要把字符串直接插入SourceManager里面，然后把sourceRange拿出来创建Comments。