NotDec: WebAssembly Decompiler and Static Analysis Framework

中文

NotDec is

1. A project that aims to demystify the internal of decompiler.
2. A webassembly decompiler that can experiment with new decompiler techniques.
   • Variable Recovery
   • Structual Analysis

中文

NotDec: 反编译器原理分析

本项目旨在：

1. 学习现有反编译器的原理，系统地总结现有反编译器的工作，算法
2. 选择合适的算法，尝试实现自己的反编译器

资料收集

学习阶段：

1. LLVM IR基础：只要达到能手写LLVM IR的程度就行。即主要理解各种语言特性对应的是什么样的LLVM IR代码。同时理解带alloca的半SSA形式，即alloca里的变量是非SSA，外面的是SSA。

   • llvm-tutor
   • ollvm源码

2. SSA与编译优化基础

   • 《Engineering a compiler》 上来先看9.3章，深入研读。其他的章节没那么重要
   • 再找找其他讲过SSA的中文书？

   关于SSA的实验

   • mem2reg 实验指导 · GitBook (buaa-se-compiling.github.io)
   • Lv9+.4. SSA 形式 - 北京大学编译实践课程在线文档 | 北大编译实践在线文档 (pku-minic.github.io)

   其他不错的资料：

   • 《SSA book》
   • 《simple and efficient ssa construction》

3. 反编译

   • 代码优化 和 变量恢复
   • 控制流结构恢复

资料

现有的反编译器和资料

规划：基于LLVM IR的反编译

为什么要使用LLVM IR？

1. 之后可以直接对接SVF，得到较好的指针分析结果。

优先实现wasm的反编译。

1. Wasm转LLVM IR
   1. WAVM是一个基于LLVM的wasm的JIT，有部分逻辑是WASM转 LLVM IR
      1. 生成的IR不够简洁，有很多为了编译到汇编的冗余的内容
2. TODO

规划：反编译阶段

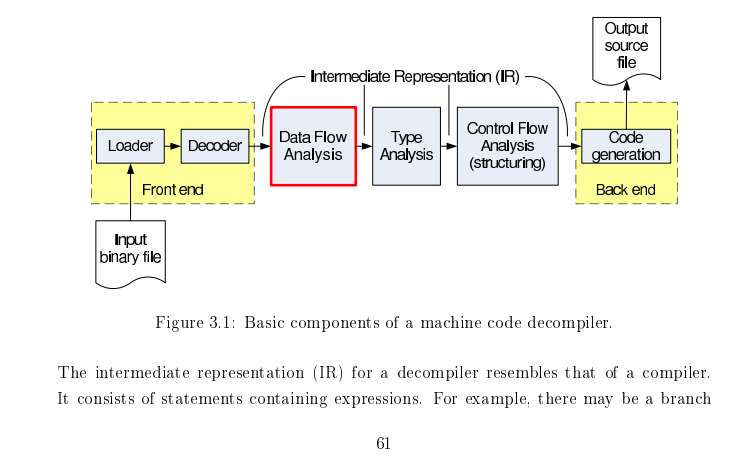
图片来自Static Single Assignment for Decompilation

反编译中的关键算法： Type Recovery（通过指令约束推导类型） Structual Analysis(恢复控制流)

1. 前端：将字节码转为LLVM IR
2. 中端：优化与分析
   1. 分析函数参数、分析callee saved register (wasm可以跳过这个阶段)
   2. SSA构建：使得前端可以有些冗余的alloca，由SSA构建来将相关alloca消除。 （编译原理相关）
   3. GVNGCM：Global Value Numbering and Global Code Motion 优化算法，有强大的优化能力，有助于反混淆等。（编译原理相关）
   4. 内存分析：将各种通过内存访问的变量显式地恢复出来。可能要用到指针分析算法，类型恢复等。关键词：Memory SSA。
3. 后端：高层控制流恢复，将字节码转为AST，打印为高级语言的形式。

项目架构与工具

由于基于LLVM IR，因此语言采用C++。

开发环境：VSCode + CMake。将Wabt，LLVM等作为CMake的外部依赖。

开发环境搭建 - DevContainer

2023年9月7日注：由于对LLVM的调试需求越来越多，项目转为使用本地源码编译的LLVM（RelWithDebInfo或Debug build），且编译得到的二进制文件过大，因此不再推荐使用DevContainer。

VSCode DevContainer。出于性能考虑，在clone时可以直接clone到wsl的ext4文件系统里。

1. 安装Docker Desktop on Windows： https://docs.docker.com/desktop/install/windows-install/ （无论是家庭版还是专业版均可）
   1. 其他系统直接安装docker
2. 用vscode打开代码，安装Dev Containers插件，按Ctrl-Shift-P 然后输入查找 Remote-Containers: Rebuild and Reopen in container.
3. 等待构建，构建完成后会直接进入开发环境中。
4. 安装CMake相关插件，toolkit选clang。

如果出现了无法使用windows侧的ssh-agent提供的ssh key的forward功能： https://stackoverflow.com/questions/72293035/error-communication-with-agent-failed-when-ssh-auth-sock-is-set-but-ssh-agent

开发环境搭建 - Linux

基于Ubuntu系统。

1. 软件安装
   • apt安装

     sudo apt install wabt python-is-python3 clang-14 cmake zlib1g-dev g++
     

   • 安装wasi-sdk到/opt

     wget https://github.com/WebAssembly/wasi-sdk/releases/download/wasi-sdk-20/wasi-sdk-20.0-linux.tar.gz -P /tmp
     sudo tar xf /tmp/wasi-sdk-20.0-linux.tar.gz -C /opt
     

2. clone 本仓库
3. 安装LLVM 14
   • 方式1：下载提前构建好的LLVM，解压得到llvm-14.0.6.obj文件夹，放到项目根目录。
   • 方式2：执行scripts/build-debug-llvm.sh脚本，下载并构建LLVM源码。中途可能遇到内存不足的情况，需要手动降低并行数量到1。 成功构建后可以将llvm-14.0.6.obj文件夹打包发送给其他人。
4. cmake build本仓库

代码调试

直接使用自带的C/C++调试，不知道为什么会非常慢，gdb执行backtrace要卡3秒，各种step命令要卡5-6秒。因此安装使用vscode的CodeLLDB插件。

代码补全使用clangd插件。根据提示禁用Intellisense，然后根据插件提示确认下载clangd。

提交代码前

1. 写好commit message，简要概况所有的修改。
2. 检查添加的代码的注释和文档是否充足。

TODO

1. 反编译器自身：能够对“内存”中的变量也构建SSA进行优化。

2. 最终的结果能够很好地重编译。

3. 反编译器实现过程尽量记录完善的文档，未来考虑整理扩写为系列教程。

4. 将wasm lift到LLVM IR

   • 支持将wasm内存直接映射到某个基地址，从而直接支持运行，以及memory grow相关指令。
   • 支持DWARF调试信息，从而映射回原wat，wasm

5. 设计一个映射，将lift之后的IR反向转回wasm

LLVM Basics

资料

书籍： Learning LLVM 12（中文版）

LLVM-Techniques-Tips-and-Best-Practies（中文版）

如何操作LLVM IR：

1. https://mukulrathi.com/create-your-own-programming-language/llvm-ir-cpp-api-tutorial/
2. 可以使用llc -march=cpp ： https://stackoverflow.com/questions/7787308/how-can-i-declare-a-global-variable-in-llvm
3. https://llvm.org/docs/LangRef.html 查询IR

中端优化：

• 实现自己的mem2reg(SSA construction)：https://www.zzzconsulting.se/2018/07/16/llvm-exercise.html
• 中端优化为什么这么神奇：https://blog.matthieud.me/2020/exploring-clang-llvm-optimization-on-programming-horror/

YouTube的LLVM频道里有很多不错的视频。

• 2019 LLVM Developers’ Meeting: E. Christopher & J. Doerfert “Introduction to LLVM”

  果然后端的水很深啊。

• 2019 EuroLLVM Developers’ Meeting: V. Bridgers & F. Piovezan “LLVM IR Tutorial - Phis, GEPs and other things, oh my! - Vince Bridgers (Intel Corporation)”》

  讲getelementptr指令讲得特别好，要是当时理解debug info metadata的时候看了这个就好了。

• 2019 LLVM Developers’ Meeting: J. Paquette & F. Hahn “Getting Started With LLVM: Basics”

  前半 讲了LLVM IR Pass需要考虑到的一些东西，users的概念，讲了移除基本块和指令时需要注意的。 后半部分讲Backend Pass也非常不错。

• 2019 LLVM Developers’ Meeting: S. Haastregt & A. Stulova “An overview of Clang ”

  讲了clang前端的架构。和之前想象中有些不一样。先是driver，然后是前端：词法分析语法分析，生成AST后codegen生成IR。

• 2017 LLVM Developers’ Meeting: D. Michael “XRay in LLVM: Function Call Tracing and Analysis ”

  非常不错的Hook介入的框架

• 2018 EuroLLVM Developers’ Meeting: C. Hubain & C. Tessier “Implementing an LLVM based Dynamic Binary Instrumentation framework - Charles Hubain

  是Quarkslab的那个QBDI，有时间真得好好学学。

• 2017 LLVM Developers’ Meeting: “Challenges when building an LLVM bitcode Obfuscator ”

  汇编混淆确实需要考虑很多情况。。

• 2014 LLVM Developers’ Meeting: “Debug Info Tutorial ”

• 2019 LLVM Developers’ Meeting: S. Haastregt & A. Stulova “An overview of Clang ”

  讲了clang前端的架构。和之前想象中有些不一样。先是driver，然后是前端：词法分析语法分析，生成AST后codegen生成IR。

• 2017 LLVM Developers’ Meeting: D. Michael “XRay in LLVM: Function Call Tracing and Analysis

  非常不错的Hook介入的框架

• 2018 EuroLLVM Developers’ Meeting: C. Hubain & C. Tessier “Implementing an LLVM based Dynamic Binary Instrumentation framework - Charles Hubain

  是Quarkslab的那个QBDI，有时间真得好好学学。

• 2017 LLVM Developers’ Meeting: “Challenges when building an LLVM bitcode Obfuscator ”

  汇编混淆确实需要考虑很多情况。

其他：

• language server
  • CppCon 2018: Ilya Biryukov “Clangd: architecture of a scalable C++ language server” - YouTube
  • Language Server Protocol and Implementation
  • Integrating with the Language Server Protocol
• 《Getting Started with LLVM Core Libraries》前端代码转换的部分
  • Getting Started with LLVM Core Libraries（中文版）

debug

打印使用llvm::outs() << xxx;直接打印llvm Value

声明全局变量

Global variable definitions must be initialized.

Global variables in other translation units can also be declared, in which case they don’t have an initializer.

• dso_local 看作是C语言的static，在同一个编译单元内

LinkageTypes

• external 是默认的，如果没有initializer就会带一个external，如果有就没有修饰符，正常的符号。

嵌套的指令 nested instrucitons

https://lists.llvm.org/pipermail/llvm-dev/2015-October/091467.html

使用IRBuilder创建的这个其实不是嵌套的指令，LLVM也不支持嵌套的指令，而是创建了GEP constant expression。这种表达式比指令更好，同时蕴含着没有副作用的语义。

PassManger

LLVM PASS的管理有两种实现

• LegacyPass Manger
• NewPass Manger

传统的LegacyPM有一些不足，例如Analysis Pass不能缓存分析的信息导致重复分析等。NewPM将Analysis和Pass做了区分。在LegacyPM中存在过多的全局变量与registries，每个Pass都需要通过宏来注册，NewPM改进了这一点，当然还有内联函数分析等其他优化。LLVM12使用的是LegacyPassManager，13之后默认使用的是NewPassManager，本项目也使采用NewPassManager。

运行与管理

LLVM API允许在应用程序中嵌入LLVM Pass，并将其作为库调用。

调试

我们基于 vscode开发，使用codelldb插件。发现无法下条件断点。

• 首先下普通断点
• 使用breakpoint list 查看断点编号
• 使用breakpoint modify 1 -c "((int64_t) (ci->getSExtValue()) < -100)"这样的命令给断点增加条件

更多使用方式见lldb使用教程

一些非常实用的调试技巧

• 打印指令，值，函数等： expr llvm::errs() << I
• 打印模块：使用定义的工具函数： expr notdec::printModule(M, "out.ll")

InstVisitor

  class MyVisitor
      : public llvm::InstVisitor<MyVisitor> {

访问逻辑：

• 名字仅有visit的为入口函数。访问模块或者函数 (Visitor.visit(M)) 会帮你访问里面的指令
• 默认继承的父类的行为：
  • 指令的入口函数 (void visit(Instruction &I)): （一般不会override）根据指令类型调用细分的visit方法
  • 各种其他类型的细分visit方法调用对应的大类visit方法 例如 visitLoadInst -> visitUnaryInstruction。
  • 最后一个大类visit方法 visitInstruction： 为空。

总结：细分visit方法是我们要override的，如果没有override实现，则会因为继承的默认实现继续分流到大类方法，最终到最通用的visitInstruction。反过来说如果override了，（如果没有主动去调用）则会截断这类指令的访问，使得这类指令不会主动调用 visitInstruction。

需要注意，如果想要visitor有个返回值类型，需要在父类模板的第二个参数指定类型，同时必须实现visitInstruction方法，因为至少要给你的返回类型指定一个默认返回值。

修改LLVM值的类型

LLVM值的类型，基于def-use关系，其实利用类型转换还是可以灵活变动。比如一个整数，虽然可能有一些加法运算，但是你还是可以强制把它设成指针类型，然后在每个使用点插入ptrtoint指令转回去。

有些LLVM值的类型，修改起来非常麻烦。尤其是函数的参数和返回值类型。函数也是GlobalValue，甚至是Constant。

打印Pass前后IR

LLVM提供了方便的 --print-after-all 等选项。首先在创建PassBuilder的时候，创建插桩的类并注册CallBack。注册所有的标准插桩后很多选项都可以生效，包括计算Pass的运行时间，是否在每个前后打印Pass，展示IR的变化diff，甚至生成HTML的报告。

// add instrumentations.
PassInstrumentationCallbacks PIC;
StandardInstrumentations SI(::llvm::DebugFlag, false, PrintPassOptions());
SI.registerCallbacks(PIC, &FAM);

现在新的Pass都继承自 PassInfoMixin 类，这个类会增加一个name函数，在运行时可以动态获取类的名称（包含namespace）。如果不确定可以在--print-after-all 后在log里查看。这个名称称为 PassID 。

命令行参数里指定的是通过PassID查找得到的缩略名称。需要提前在 PassInstrumentationCallbacks 中注册：

  PIC.addClassToPassName("notdec::LinearAllocationRecovery",
                         "linear-allocation-recovery");
  PIC.addClassToPassName("notdec::PointerTypeRecovery",
                         "pointer-type-recovery");

此时就可以在命令行中指定相关的pass打印了。比如 --print-before=pointer-type-recovery 。

Clang

AST handling

• 创建AST时有两种方式
  1. 使用Create方法，如clang::FunctionDecl::Create(...)
  2. 没有Create方法时，使用ASTContext的new操作符。如：new (ASTCtx) clang::GotoStmt(...)

CFG handling

CFGBlock包含：

• LabelStatement，用于生成Goto语句。

• 一系列语句

• CFGTerminator

  • 对于return/unreachable：保存对应的返回语句或函数调用语句。
  • 对于br/switch，保存对应的条件表达式。同时保证successor的顺序：本来CFG保证的是If-Then-Else顺序，但是如果是条件跳转，我们使用True-False的顺序，和IR里的successor()顺序一致。

• CFGBuilder在LLVM中是逆序创建的，即逆向遍历AST，逆向创建语句。在打印或者遍历CFG块的时候，其中CFGBlock::ElementList把正常的iterator改用reverse_iterator实现。存储的时候是逆向存储，但是后续读取每个CFGBlock的时候也被偷偷改成逆向读取。但是我们算法如果不是逆向的话，想要在末尾继续插入语句，反而需要插入到开头，内存开销增加了。

  • 如果将结构恢复算法弄成逆向的，首先找到所有的没有后继节点的结束块，每个结束块分治。

• 对于if (A && B && C)，CFGBlock->getTerminatorStmt()会在C处返回整个A && B && C表达式。调用getLastCondition()，会把CFGBlock最后一个statement转换成Expr返回。

BumpVector Memory Allocation

Clang的内存分配都是通过ASTContext进行的，内部使用了一个BumpAllocator，Bump是一种简单的线性内存分配，内存不会真正被释放，放弃内存复用。或者等一整块分配结束之后，再整块全部释放。根据这里，ASTContext解构时释放所有存储AST节点的内存。

• 根据这里，从这里分配的相关的数据结构内部不能有std::vector或者SmallVector这种会在堆上分配内存的数据结构。因为不会调用destructor，导致堆上的内存不会被free，导致内存泄露。

BumpVectorContext存储了一个llvm::PointerIntPair<llvm::BumpPtrAllocator*, 1> Alloc;，这是一个指针低位复用的数据结构，可以理解为一个指针加一个bool值。用户传入外部的allocator，比如ASTContext的，完全不释放内存。也可以让它新建一个allocator，并在解构的时候释放所有内存。

Clang CFG内置了一个BumpVectorContext，解构时会释放所有内存。因此在结构分析过程中，CFG相关的基本块虽然出现创建后又删除的情况，但不会导致内存泄露。 TODO: 一些临时的AST节点，如一些临时的Goto语句，它们的内存释放怎么办？

这次在BumpVector里增加的erase函数，仅把元素移动到末尾然后解构，和内存泄露应该无关。

clang::QualType

QualType 本质上就是一个指针，同时复用了低位的bit位，存储一些qualifier信息，如volatile等修饰符。

• QualType大部分情况下可以看作是clang::Type*
• QualType有可能为空指针，同时也可以直接创建空的QualType

clang::IdentifierInfo

IdentifierInfo除了名字字符串之外，仅仅存储了一些名字的种类信息，例如是不是define的，是不是keyword，是不是variable或者function name。

• 变量重名：它似乎并不对应作用域，并不用于检测变量重名。
  • Sema::LookupName 内部手动遍历检测了重名情况。

NotDec Development Document

NotDec的项目文档。

反编译器前端

现有的反编译器内部算法往往是通用的，仅需要编写新的转IR即可支持新的语言。

WebAssembly Frontend

wasm frontend 负责将WASM字节码转为LLVM IR。

LLVM的好处就在于可以先生成比较差的IR，然后通过优化Pass不断修补。

WASM 现有工具

1. WAVM也是一个基于LLVM的带JIT功能的runtime。C++编写
   1. WAVM\Lib\LLVMJIT\LLVMCompile.cpp LLVMJIT::compileModule这个函数应该是编译入口点，很多可以参考。
   2. WAVM\Lib\LLVMJIT\EmitFunction.cpp EmitFunctionContext::emit 编译每个函数。关键是decoder.decodeOp(*this);这句，会根据不同的指令访问对应的同名函数，比如看WAVM\Lib\LLVMJIT\EmitCore.cpp，遇到block指令会调用EmitFunctionContext::block函数。
2. aWsm 也是一个基于LLVM的带JIT功能的runtime。虽然是rust写的，但是还是用的LLVM C++ API，转换相关的逻辑也都是可以抄的。
3. WAMR wasm-micro-runtime 基于LLVM的，但是是C语言，使用LLVM-C-API，我们打算用的是C++的API。
   1. 真的是自己写的字节码解析器好像。。。wasm_loader.c wasm.h
   2. 有相关wasm到LLVM IR的转换可以参考：aot_llvm_extra.cpp

代码架构

• wasm模块解析器：基于wabt。wasm-c-api不太行因为是用来embed一个WASM VM的。

  • 目前直接通过
  • 未来考虑通过find_package直接使用： https://github.com/WebAssembly/wabt/pull/1980

• 首先由于最后都是转IR，所以BaseContext保存LLVM相关的Context。其实可以作为全局变量，为了以后可能的并行，把这类全局变量都搞到一个类里。

• wasm::Context是相关生成的代码依附的数据结构，保存比如wabt::Module这种Context。为了方便应用，增加了对BaseContext的引用，对llvmCtx的引用等等。

Specification

需要了解LLVM IR的语义：

1. LLVM Language Reference Manual
2. 2019 EuroLLVM Developers’ Meeting: V. Bridgers & F. Piovezan “LLVM IR Tutorial - Phis, GEPs ...” - YouTube

和WASM的语义：Modules — WebAssembly 2.0 (Draft 2022-09-27) 注意现在直接翻标准是新release的2.0标准了。我们暂时先支持1.0标准，wabt现在也仅支持1.0，如果文件头里写version为2会报错。1.0的标准可以看这里。 不确定每个指令的语义，看这种地方。

1. 名字比较难处理，wasm的name section允许重名，而且wasm中因为是二进制格式，理论上名字可以取任意utf-8。那边wat格式的定义也有类似的问题。但是wabt似乎已经处理了相关的问题？
   • 在src\binary-reader-ir.cc里的BinaryReaderIR::GetUniqueName函数，如果重名了会加数字后缀。
2. 类型：i32 i64 对应LLVM中的i32 i64, f32 f64对应LLVM中的float double。
3. 每个wasm的Global值转为llvm中一个的global值。相关访问只有Load和Store指令。
   1. 名字直接使用wabt那边传过来的名字 名字更改为global_<ind>_<original_name>这种格式，即在原来名字前加上前缀标识。
   2. Linkage Types 选择internal。被导出的更改为external。
   3. 根据mutable，设置llvm那边的const属性
   4. 处理init_expr
4. 内存：转为一个global数组，u8 array。
   1. 内存初始化：似乎LLVM IR里一个数组不能部分初始化。很多0也没办法。就这样吧
   2. 内存访问：计算关于u8的偏移（get element ptr），然后再转为对应的类型指针load出来。即LLVM中[大数字 x i8]类型。因为只是分析，所有不用考虑内存增长的事情。
5. 函数
   1. 每个Local转化为函数开头的一个alloca。
   2. 非直接跳转 callind

指令、栈、控制流的处理

参考WAVM，见顶部现有工具一节。参考栈验证逻辑。能保留的最好直接解码为SSA。这里的block直接考虑Multi Value Extension，防止以后架构需要重构，但是函数返回多个值的先不支持。

• 每个栈上元素对应一个SSA的Value。某种形式上可以维护一个Value栈（作为局部变量，不需要作为Context）。
• 控制流跳转维护一个block的嵌套栈，保存br时跳转的目标。关键是如何在找到跳转目标的同时，把栈弹到对应的值。
• 处理Block的时候，这里用递归和用栈都可以。选择用实现起来更简单的递归。aWsm好像是递归的写法，WAVM好像是用栈，复杂一点。
• loop和block的区别在于，给phi赋值，然后用Phi替换栈上值的地方不同。一个是基本块开头，一个是基本块结尾
• 函数体大致也算一个Block块，但是labelType写Func。

控制流指令的处理，与SSA生成

visitFunction：

1. 创建allocaBlock，分配参数和local空间

2. 创建alloca -> entry边，创建return块备用

3. 调用visitBlock函数（visitBlock函数必须把所有的结束跳转都引导到exit块）

4. 创建结尾的return指令。（visitBlock内部处理的时候只有br，return也看作特殊的br，函数只允许在结尾返回）

递归的基本块生成算法visitBlock： 要求与保证：

1. 要求算法的整体表现类似于给定类型的单个指令
2. 要求调用者提供的entry和exit中，需要创建Phi的那个为空基本块（但是可以有Phi指令），便于创建Phi节点。
3. 保证结束的时候跳转到exit块。不会有其他控制流。

注：

1. 没必要再用一个额外的stack防止访问更深元素，因为调用过了wabt的validate

调用visitBlock前，根据block类型

1. Block类型：创建新的exit块，替换原来exit，处理完毕后新的exit作为entry继续生成指令，旧的exit还是exit
2. Loop类型：创建新的entry块，替换原来entry。loop结束也一样。

visitBlock：

1. 先创建好跳转目标，Phi节点，用这些设置好BreakoutTarget结构体，压入栈中：
   1. 根据是loop还是block类型的块创建Phi。如果是Loop，直接把当前栈上的值弹出来，作为phi的operand，然后把phi push回去，替换。如果是block，先创建空的Phi。（等后面结束的时候再从栈上加operand。
   2. 保存当前value栈的情况。
2. 依次遍历每个指令生成。
   1. 普通的指令根据指令语义，从value stack中取值，
   2. 如果遇到了跳转指令：
      1. 如果跳转的目标是普通基本块，则从栈上取值加入到对应的Phi中，
3. 块结束的时候，不需要主动跳转到exit，因为exit不一定是当前block的exit，因为在Loop的情况下，结尾没有额外创建基本块，所以不需要特殊处理。Block结尾的跳转交给外面处理。
4. Block结束时，在end前，处理隐含跳转到结束块。由于类型检查，不会有多余的值，不需要unwinding弹出栈。

控制流指令的处理：

1. br指令，其后是stack可以是任何类型。为了处理这种情况，我们直接增加unreachable标识，无视这些指令。
   • 对于Block
   • 对于Loop，由于结尾是从Loop离开的唯一方式。如果有br指令封锁了结尾，则不可能从这个loop结尾离开了。此时直接保留UnReachableState
2. block，loop分别对应在结尾，开头，增加一个label。注意到block只需要为return的值创建Phi，loop需要对参数创建Phi。
3. if对应一些label和br_if，br代表直接跳转，br_if同理，根据语义找到对应的跳转目标，生成条件跳转即可。
4. br_table看似比较麻烦，看了下和LLVM的switch语句对应得非常好啊。也是根据不同的值跳转到不同的边。

最开始的时候先写一个类型检查，打印出每个指令后当前栈上的类型情况的代码，然后再加生成相关的东西。

wabt那边代表Block的结构体看wabt的src\ir.h 383行struct Block这边。

• std::string label 直接放到BasicBlock的名字里面
• BlockDeclaration decl 和FuncDeclaration是一个类型
• ExprList exprs
• Location end_loc 代表输入文件里的位置，暂时不管，除非后面想加debug信息

多个参数和返回值的时候，顺序：

• 函数参数逆序遍历（pop），同时从栈上pop出来。
• 函数返回值顺序遍历，同时push到栈上。

查OpCode看wabt/include/wabt/opcode.def。Opcode和ExprType之间的关系看src\lexer-keywords.txt，或者看wabt/src/lexer-keywords.txt里面对应的Opcode创建了什么Expr，或者看src\binary-reader-ir.cc里找对应的指令到底创建了哪种Expr类。

这里面的类继承关系看 src\ir.h。其实就是搞了一个ExprType，然后在onXXX指令的函数处直接创建了这个类型的Expr，导致opcode和expr之间没有明确的对应关系。

运算指令的处理

• 简单的可以对着这个找指令https://llvm.org/docs/LangRef.html。
• 可以找llvm intrinsic，例如fabs指令使用了对应的Intrinsic::fabs
• 更复杂的可以自己手写llvm函数，然后直接调自己写的函数，之后看看要不要内联什么的

资料：

• WAMR里，intrinsic的实现 https://github.com/bytecodealliance/wasm-micro-runtime/blob/d309091706f2fbfc3ccca2907226f57db4d612f3/core/iwasm/aot/aot_intrinsic.c
• WAVM里，intrinsic的实现（使用irBuilder） https://github.com/WAVM/WAVM/blob/79c3aa29366615d9b1593cd527e5b4b94cc6072a/Lib/LLVMJIT/EmitNumeric.cpp

比较 - 浮点数

参照https://www.w3.org/TR/wasm-core-1/#-hrefop-feqmathrmfeq_n-z_1-z_2 和https://llvm.org/docs/LangRef.html#id309 对比语义

1. feq在wasm中，如果有nan就返回0，反过来只有无nan才返回true，所以采用fcmp oeq。
2. 而fne，有nan就返回1，所以要用fcmp une

SIMD

参照 https://github.com/WebAssembly/simd/blob/master/proposals/simd/SIMD.md 指令 https://github.com/zeux/wasm-simd/blob/master/Instructions.md https://nemequ.github.io/waspr/instructions

指令格式

{interpretation}.{operation}

前缀{interpretation}表示如何解释 v128 类型的字节：格式为{t}{lane_width}x{n}

• t是类型: v（只划分不解释）/i（整形）/f（浮点）
• lane_width是lane位宽：8/16/32/64
• n是lane总数

处理

1. 默认的v128在LLVM IR中被定义为<2 x i64> 类型。
2. Wasm指令中的vector操作数都是v128类型，{interpretation}则是指令执行和执行完的向量类型，所以需要使用BitCast进行转换。过多的BitCast显得很繁杂，参考了WAVM使用宏定义来简化代码。
3. LLVM中的Intrinsic对vector支持很好，直接转换好数据类型后调用对应的Intrinsic即可。
4. 有些指令设计向量的缩减与扩增，可以用Shuffle配合mask来实现。

链接

• WebAssembly Object File Linking： https://github.com/WebAssembly/tool-conventions/blob/main/Linking.md
• Adventures in WebAssembly object files and linking： https://mike.zwobble.org/2021/04/adventures-in-webassembly-object-files-and-linking/

相关section的解析可以看src\binary-reader.cc里的BinaryReader::ReadCustomSection函数。

测试

1. 基于sysY语言的测试用例，自动编译为wasm和wat格式，反编译到IR后和sylib.c得到sylib.ll一起输入lli执行。验证输出的正确性。
   • 使用-c编译为未链接的object ？
     • 缺点1：内存是导入的，大小不确定
     • 缺点2：需要处理额外的。
   • 编译为完整模块，加上-g -O0 --no-standard-libraries -Wl,--export-all -Wl,--no-entry -Wl,--allow-undefined等选项。全部导出可以不用特殊处理main函数的导出，allow undefined好像会让没定义的都变成导入。
     • 目前暂时的方案。

其他

Wasm中的函数指针调用（复习）

在二进制模块中有id为4的table section。里面有一系列的table类型，初始化则由element section负责。table类型有两部分，reftype和limit。limit应该是类似数组大小的东西，但是同时包含了上限和下限。

reftype其实就是个enum，表示是不透明的external类型还是function类型。即，光是table section里，有用的信息只有定义了index，给每个index处的table标明了上下限。

reference类型是和其他类型独立的。即真的无法观测到底是怎么表示的，只能被存在table里。即和程序call指令里面用的index不同。其实我们只要管func ref，external ref一般指不是函数的情况。如果有的话直接那个吧。

接下来看elem section。它可以是passive的，即等着被table.init指令使用，用来初始化某个table。或者是active的，直接初始化某个table。最后可以是declarative的，说是前向声明。（TODO，不是特别理解）

现在直接翻标准是新release的2.0标准了。我们暂时先支持1.0标准里面流行的active类型的elem。（wabt现在如果文件头里写version为2会报错。（这个version是在整个二进制模块的header处定义的。）但是依然支持这一部分的新格式，可能是以支持相关拓展的形式实现的）

首先介绍标志位：

• bit0: passive 或 active 的标志位。
• bit1: 分两种情况
  • active: 存在额外的table index。（否则默认是0）
  • 标志位表示是passive或者declarative。
• bit2: bit 2 indicates the use of element type and element expressions instead of element kind and element indices.

elem section由三部分组成：

1. table index, 初始化哪个table。目前因为只有一个table，所以必须是0。
2. offset, 常量表达式，即一些指令。例如：41 01 0b解码为i32.const 1; end;。
3. vec(func ind) 一系列函数下标，表示要初始化成这些。

Features to add after the MVP - WebAssembly 中文网|Wasm 中文文档 https://www.w3.org/TR/wasm-core-1/#element-segments%E2%91%A0 （可以在这个页面搜索at most one） 这里提到了，MVP标准中wasm最多有一块内存，最多有一个table。

对应到LLVM IR的关键是，相同的语言特性会怎么在LLVM IR上实现/怎样的LLVM IR会编译到这样的wasm。LLVM里只有Call指令，但是参数是一个函数地址的value。目前看来可以搞一个函数指针数组，对应初始化后的table。然后将callind翻译为从函数指针中取，然后再call。

至于非直接跳转，由于和llvm的switch完美对应，就非常简单。br_table指令会带有个table，让index从1到table的大小遍历，根据当前栈上的值是否等于当前index，从table里面取出要跳转的层数，找到对应的基本块，为switch增加跳转目标即可。

TODO

最好能实现单个函数的反编译与混淆，即转换回Wasm时最好能保证其他部分不变。。。如果使用LLVM自己的wasm后端好像有点复杂

Docs of optimizers

项目使用LLVM Pass框架来进行反编译中的中间代码优化。

LLVM Pass入门资料

入门教程banach-space/llvm-tutor: A collection of out-of-tree LLVM passes for teaching and learning (github.com)

中文文章[翻译]现代化地编写LLVM Pass -- part I-外文翻译-看雪论坛-安全社区|安全招聘|bbs.pediy.com (kanxue.com)

变量恢复

• 优化：wasm解析为IR后先优化一下，对后续反编译有好处。运行LLVM的一系列代码优化，包括SSA构建（Promote）。
• 全局栈指针识别：在第一个基本块，在任何内存访问之前，是否对全局变量进行了一读一写的修改，且写的是读出的值加一个常量。是的话就认为是栈指针。如果大于等于一半的函数是同一个栈指针，则标记它为全局的栈指针。
• 指针识别：基于已有的指针类型，运行基于Datalog规则的指针类型分析，将所有替换为指针。
• 类型识别：基于Retypd，

栈指针识别

背景：根据《An Empirical Study of Real-World WebAssembly Binaries: Security, Languages, Use Cases.》这篇paper，有约一半的wasm都使用global 0作为栈指针。这说明针对栈指针的分析的重要性。这也是向更通用的算法拓展的一步。

算法：在第一个基本块，在任何内存访问之前，是否对全局变量进行了一读一写的修改，且写的是读出的值加一个常量。是的话就认为是栈指针。

局限性：可能出现加载栈指针后，先存在局部变量里读出再sub的情况。我们通过在分析前调用 Promote 这个SSA构建的pass，缓解这个问题。

指针类型识别

为了简化考虑，把一切都平坦化，假定栈大小固定，则可以看作栈上都是普通的基本类型变量。不考虑数组，把数组看作是结构体的特殊情况。不考虑数组下标，都看作是指针的整数加减运算。

背景：在二进制层数字和指针是混在一起的。因此往往需要把未经分析的值看作比如undef32类型，然后在分析过程中设置为更细分的数字类型和指针类型。可以看作是一个类型的lattice。

类型分析是少数可以用数据流术语表达的问题之一，并且是真正双向的。

1. 定义的类型影响使用的类型
2. 使用的类型影响定义的类型：
3. 库函数调用（看作使用）影响之前的定义，已知返回值类型的赋值影响之前的定义。引用参数调用影响之前的定义。

wasm指针：现在内存不是直接访问的：即load和store指令会在加载和保存的时候，将偏移加上mem0的基地址。但是，如果一旦引入了类似于直接alloca的这种情况，则它将是直接地址，而不是直接加上mem0的基地址。问题在于，可能会有指针混指的情况，即可能指向全局变量或者栈空间变量。这样在后面load/store的时候，无论是加上mem0的基址还是不加都有问题。因此引入地址空间的概念。将wasm的内存指针单独分离出来，成为独立的地址空间。

算法：双向的传播问题，可以用传统的数据流分析实现，但是较为复杂。先使用Datalog进行原型设计，后期再改进。

• 加法运算：数字加数字，指针加数字，数字加指针，三种情况。
  • 如果运算的参数中有指针，则结果也是指针。
  • 如果发现了一边是指针，另一边大概率是整数类型，同时结果类型也是指针类型。
  • 反向推导：如果运算的结果是指针类型，则里面至少有一个指针类型。
    • 如果已知某个参数是整数，则另一个参数为指针类型
    • 如果已知某个参数是指针类型，则另外一个参数为整数类型。
• 减法运算：数字减数字，指针减数字，指针减指针（小概率），指针减法运算
  • （如果不考虑指针减去指针）第二个参数是数字类型。
  • （如果不考虑指针减去指针）第一个参数是指针类型，结果也是指针类型。
  • （a-b=c）如果a是指针，b是数字，则c是指针
  • （a-b=c）如果a是数字，则b和c都是数字
  • （a-b=c）如果b是指针，则a是指针，c是数字

变量访问识别

进一步识别每个内存访问，以及涉及的加法运算。

• 加法运算：某个类型的某个偏移出

结构体的识别的关键在于，我是从谁那里，加了一个偏移。一般是从栈指针，但是一旦是从别的变量那边加出来的，这时候可能就代表着结构体。

实现

• 识别并消除函数开头和结尾的栈指针操作
• 把对mem0的取下标+load/store操作，根据全局变量还是局部变量，转变为（新创建的）局部变量或者全局变量的操作。

清除IR中的全局栈指针，并对其使用处的指令操作数(局部变量地址)进行转换，转换为对alloca里的东西的使用，把对mem0的使用，其中的使用mem0的栈部分，改为使用我们的alloca。

变量分为全局变量，局部变量，堆变量，堆变量一般直接调函数分配，暂时不考虑。

• 全局变量的访问：对mem0取下标的这个值是常量（范围大致在1024到一个很大的值之间）【可能存在偏移运算】
• 局部变量的访问：对mem0取下标的值，是栈指针（取global 0）【可能存在偏移运算】
• 也可能直接把地址存入变量里，即取地址。

其中偏移运算可能是常量也可能是变量，是变量时甚至可能存在乘法运算。 （如果把栈指针存到了结构体里怎么办？假装它没有定义结构体，定义了很多零散的变量？）结构体的问题在于，成员地址可能基于结构体自身的指针计算得到

• 如何判断global0是不是栈指针
• 如何匹配函数开头的栈指针的sub操作
• 如何判断哪些值是栈内存的指针

如何判断哪些值是栈内存的"抽象解释"算法

和传统的数据流分析不同的地方在于，LLVM是SSA形式，每个值只有一个赋值点。因此，一个值要么是栈指针，要么不是。因此只需要直接循环迭代。但是LLVM里还是有变量，即alloca出来的值，可能因为控制流的跳转而来自不同的取值，从而导致基于变量计算出来的值，依赖于这个变量是不是和栈指针有关的东西。

要分析清楚对mem0取下标的这个值，是不是来自stackpointer的运算。

1. 一定来自stack pointer
2. 可能来自stack pointer
3. 一定不来自stack pointer

为每个llvm的Value维护一个bool类型变量表示是否是栈指针。 遍历所有基本块（可能拓扑排序会高效一点），直到某次完全遍历也没有任何变化 初始化：算法开始前已经判断了函数开头的栈指针值，对应的bool设置为true 如果遇到了运算，任意一个输入值对应true的话，结果也设置为true。

把变量也标为是栈指针类型？所有对这个变量的load都是栈指针？

union怎么办？先不考虑。

目前的解决方法： 遇到内存访问指令沿着use-def向上回溯，构造一条chain 看是否可达sp,如果可达，那么就是栈地址，并把它放在栈相关集合中。 如果存进去的值也是栈地址，那么就把对应偏移的放在另一个栈相关集合中。

TODO:

1.需要实现过程间分析，如果call指令的参数和返回值都是栈地址，需要把它们放到栈相关集合中。

能否保证语义安全？因为我们现在转出来的IR是能跑的，如果变量恢复后，是不是就不能跑了？比如部分变量识别失败，还是存到mem里去了。

反编译器后端 - 结构分析

结构分析负责将IR转换为伪C代码。

使用Goto语句的IR转C

• 给所有的基本块前添加标号，对于任意控制流跳转，使用goto实现。最后删除无用的标号。

这种方法可以考虑作为现有算法的辅助，将算法无法处理的边转换为Goto语句。算法可以自由选择能够折叠的边进行折叠，从而只需要考虑实际的结构分析效果，不必纠结算法的完善和鲁棒性。

Structural Analysis 和 Reducible Control Flow

• PPT(结尾介绍了Reducibility)
• PPT(介绍了Reducibility编译原理相关的内容)
• PPT:介绍了structural analysis 特别说明了
• PPT:更详细地介绍了structural analysis
• 介绍了T1 T2转换

一个CFG如果是Reducible的，则我们可以将图上所有边分割为两部分，前向边，和反向边

• 前向边构成有向无环图，每个节点可以从entry到达。
• 反向边的目标节点都支配源节点。

定义2：T1 T2转换 一个CFG如果是reducible的，可以通过规则将图中的节点递归缩减为单个节点。

• T1 自环可以被缩减
• T2 如果某个节点仅有一个前驱，则可以将该节点缩入这个前驱节点

然而，有个PPT里面说，这种T1 T2转换，对控制流的缩减，从而对控制流划分的层次结构，不一定规范地符合真实源码里面的划分。T1 T2转换是最早的，最简单的一种interval analysis.

Structural Analysis For Dataflow Analysis

相关资料

• 《A Structural Algorithm for Decompilation》反编译的结构分析
  • 在一个CMU的lecture notes里面提到了这个paper
• 《Advanced Compiler Design and Implementation》 非常经典的编译器理论书籍
  • Phoenix论文里，提到结构分析的时候，也推荐了让读者去看这里。因此非常值得读一读。
  • 在203页更详细地介绍了structural analysis。建议从196页的Reducibility开始阅读。（书里面的页码，不是pdf的页码）这些结构分析都比较老了，而且有的不太是为反编译设计的。

概述：在编译优化方面，有研究人员提出，要是在IR（CFG）层面能够用上AST层面的信息（IF，While，For控制流结构），能够加速现有的数据流分析。然而在IR（CFG）层面，高级语言的结构信息已经丢失了。因此，有部分研究人员提出了通过模式匹配的方式，从CFG中识别出控制流结构。由此诞生了interval analysis算法，后续发展出了Structural Analysis。

结构分析一般可以分为一下几个步骤：

1. 类似interval analysis的嵌套区域划分。
2. 将划分好的子区域进行模式匹配，匹配为高级语言的控制结构。

定义：(Maximal Interval)：最大的，单入口子图，（假设入口节点为I）且子图中所有闭合的路径都包含I。

定义：Minimal Interval：是指：(1) 一个natural loop，(2)一个最大的有向无环子图，(3)一个最小的不可规约区域。和maximal interval主要区别大概在于，maximal interval划分loop的时候会把连带的有向无环分支带上，而minimal interval会单独分出来。

一个minimal interval和maximal interval的区别如下：左边是maximal interval的划分，右边是minimal interval的划分。

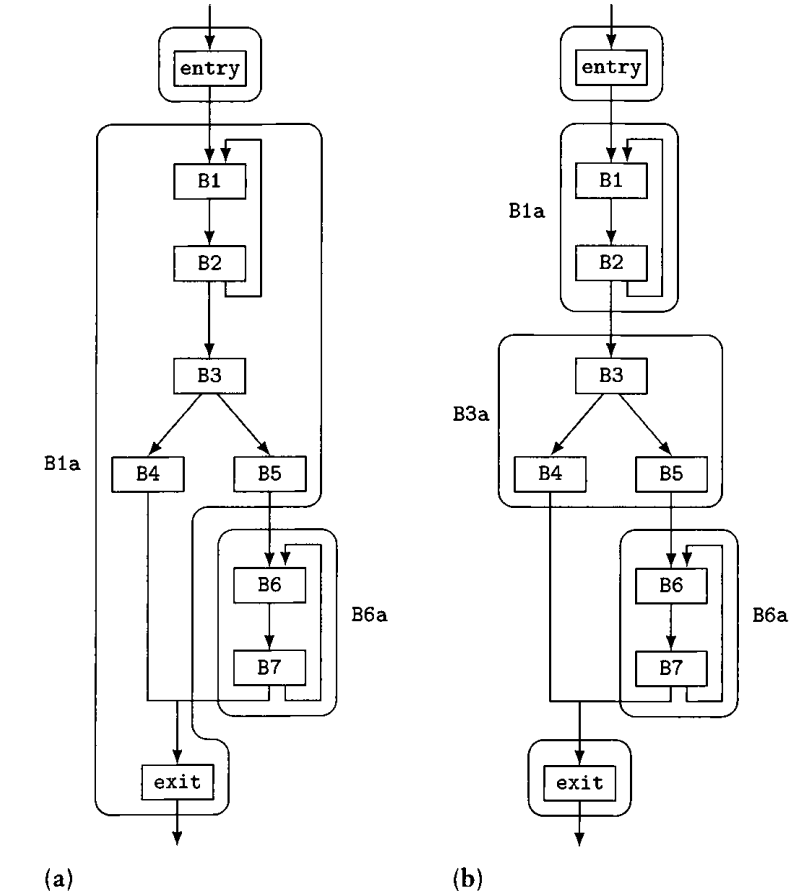
定义：Natural Loop 背景：在编译原理里面的loop，也是希望仅有单个节点支配整个loop。我们使用支配关系寻找loop的时候，由于它是一个loop，因此必然至少有个“反向边”，不然构不成一个环。 Natural Loop的关键在于那个反向边，即头节点支配尾节点的边。

一个反向边的Natural Loop（即，natural loop严格说并不是一个单独的概念，反而是对一条反向边而言的。），是指，最小的，包括反向边头和尾节点的节点集合，集合内所有节点的前驱，要么在集合内，要么这个节点是entry节点，前驱是entry的前驱。

当你移除那个entry节点的时候，因为entry节点支配其他节点，图就被分裂成了两部分。此时寻找所有有路径到达t的节点（t这里指反向边的源节点），这些节点和entry节点构成了natural loop。

在《A Structural Algorithm for Decompilation》里直接使用了类似T1-T2规约的方式划分interval。

Interval Analysis (maximal interval)：该算法就是《A Structural Algorithm for Decompilation》里面用的，算法如下：

迭代性：该算法是一个迭代的算法，每一次迭代找出节点集合后，即使可以看作一个新的单个抽象节点，也不会产生新的节点集合包含这些本轮生成的抽象节点了，这些Interval嵌套的情况是由下一轮迭代负责的。（图片里的算法不包含这个迭代，迭代在另外一个没截图的算法里）

步骤：

• 从entry节点开始，依次类似T1 T2规约的方法（即，“看是否某节点仅有一个前驱”的拓展版，看某节点的前驱是否都在集合里）把节点加入集合中。如果结束了，就从当前集合的后继节点里抓节点出来再进行这个过程。直到所有节点都被归入了某个集合。
• 更新H的那一行代码的意思是：加入H的新节点，(1)不属于当前规约好的集合，(2)直接前驱在当前规约好的集合里。 （即，按顺序弄。）

在《Advanced Compiler Design and Implementation》里提到这种方式划分的是Maximal Interval。书中还提出了改进版的算法，划分的是Minimal Interval，划分效果更好，更小的区域便于后续划分高级语言的控制结构。

Interval Analysis (minimal interval)：该算法是《Advanced Compiler Design and Implementation》提出的改进版。它将CFG划分为三个部分，无环（acylic），natural loop和improper region。无环部分即有向无环子图，其他两种区域则包含环。

• proper region和improper region：proper region指一些虽然无环，但是也不能被简单的if-else等结构匹配的无环部分。improper region与之对应，有环，但是是比较复杂的环。

步骤：

1. 使用一个后序遍历找到loop header，和improper region的header。（后面再详细解释）
2. 对每个loop header构建natural loop区域。(使用支配图，判断是否有前驱节点指过来的边是反向边，即head dom tail)
3. 对improper region的header构建minimal SCC。（即只把环分离出来）
   1. 构建区域之后，对（区域的）所有的直接后继节点构建最大的有向无环子图（把环上长出的分支分离出来），如果成功弄出节点数量大于1的子图，就构建一个有向无环区域。
4. 递归整个过程直到终止。

可以感受到，这其实是基于前一个算法，融合了把有向无环的子区域分离的想法。同时还顺便分离了有环区域中的natural loop。（但是，有一些具体的实现细节也还是不清楚。。）下面详细解释算法细节。

背景1 深度优先遍历与逆后序遍历： Depth First Spanning Tree 是在DFS遍历过程中生成的一个树。基本思想是，DFS遍历过程中，会出现一种情况：判断当前节点指向其他节点的一条边的时候，发现这个边指向的目标节点已经被访问过了，所以就不需要沿着这条边过去了。因此可以将边划分为遍历使用了的边，和遍历过程中没有使用的边。

在深度优先遍历时，怎么才算是反向边？当然是这条边指向了已经被访问的节点。即遍历时发现指向的地方已经访问过了。这个过程并不是确定性的：即，也有可能出现，根据选择的子节点不同导致反向边不同的情况。比如两个子树交叉指向隔壁子树的更高的节点。深度优先遍历的时候，走过的边属于前向边（forward）。如果某条边反过来就属于前向边，则它是反向边（和某个前向边形成2节点的小环）。剩下的边属于交叉边。

是否完全确定反向边？：在《A Structural Algorithm for Decompilation》里直接使用了类似T1-T2规约的方式划分interval。后面判断是否是loop的时候提到，只需要检查interval的header的前驱指过来的边是不是反向边。而且只需要看后序遍历的顺序上的关系即可。我们这里探讨的问题是：**（检查interval header的predecessor）真的只需要看后续遍历的顺序就可以确定是否是反向边吗？**反向边的定义是，head节点支配tail节点。假如我们有个interval，有个back edge，如果想破坏这个支配关系的同时，保留后序遍历的顺序。假如根节点在DFS优先遍历左子树，我们的interval也在左子树，我们从右子树引一条边过来，这样不会影响左子树节点在后序遍历的顺序。同时我们把边指向header到tail节点的路径上，这样head就不再支配tail了。这样不就破坏了这个关系了吗？除非，这样引入的边会破坏interval的划分。确实，我们考虑那个被指向的节点，这个节点之前之所以会被归到这个interval，是因为它的所有前驱都在interval里了。这样增加的边会影响interval的划分，因此我们没能找到反例。

结构分析算法(《Advanced Compiler Design and Implementation》) 这边书中的算法是基于最早的结构分析《Structural Analysis: A New Approach to Flow Analysis in Optimizing Compilers》的改进。它的区域类型有：Block, IfThen, IfThenElse, Case, Proper, SelfLoop, WhileLoop, NaturalLoop, Improper这几种。

算法的大体结构如下：（书中205页）

1. 使用一个DFS_Postorder算法，给每个节点标上序号。
2. 在一系列的节点遍历中，不断辨识出新的区域，把这些区域规约成单个抽象节点（因此可能需要修复图结构，并且可能需要重新做后序遍历）。
   1. 规约时，把进入区域的边，离开区域的边作为这个抽象节点和其他节点的边。
3. 直到最后规约为仅一个节点。

Structural Analysis For Decompilation

概述：

然而，上面介绍的，为数据流分析加速设计的结构分析，用于反编译有着根本性的缺点。

1. 仅识别了一些简单的图模式。虽然通过递归，能够识别这些模式的组合，但当出现了复杂的图的时候，会完全放弃识别。无环图被识别为Proper Region，有环图被识别为Improper Region。
   1. 这对数据流分析算法没有影响，因为没识别出来可以按照旧的方式分析，只不过无法加速了。然而，这一点对我们反编译非常致命，直接放弃了划分。
      1. Phoenix在usenix 2013提出了，可以将部分边转成goto，从而能够继续识别出更多的控制流结构。
2. 本质上，稍微复杂一点的CFG，确实就不能识别控制流结构了。

SESS

**Single entry single successor (SESS)**分析

来自《Enhanced Structural Analysis for C Code Reconstruction from IR Code》论文中的3.3节。（论文中3.1、3.2回顾了一下什么是结构分析）。

背景：结构分析其实没有考虑break，continue等跳转指令。带有这些跳出语句的，也可能被归类为proper/improper region。

定义：假设有一个CFG，内部划分了SESS区域R，唯一的entry节点是r，successor节点是s，则有以下性质：

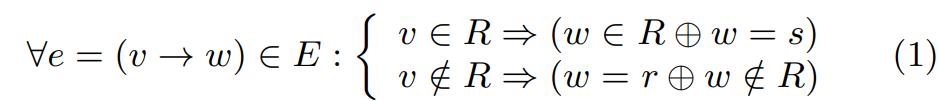
SESS区域：entry r属于region，successor s不属于区域内（看作区域的线性后继块）。

• 对于（整个图的）任意边，如果source属于区域内
  • 要么target属于区域内，区域内部边
  • 要么target等于successor节点
• 如果source不属于区域内
  • 要么target是entry节点（进入）
  • 要么target不属于区域内（区域外部边）

有哪些边被否认了？区域内部到区域外部的，不经过entry和exit的边。

Tail Region：文中提出了Tail Region的概念，它为现实中break的情况设计。一个带break语句的基本块，原本有一个很难处理的跳出的边。有了tail region之后，把它识别成tail region，就暂时假装没有那个边，继续做相关分析。

一些其他点：

• 论文中提到有这些性质的区域可以直接输出为C语言代码。因此SESS算法的目的是让SESS区域覆盖尽可能多的边。
• 在原有匹配cyclic region，acyclic region之后，如果匹配失败，就尝试匹配tail region。这里在Phoenix里面提到，这篇论文里没有写清楚具体的匹配算法。而且他们发现，经常确实也匹配不到这种tail region，如果图太复杂还是会失败。
• 关于论文没有说清楚的其他点，首先是怎么识别SESS region吧，可能是在原有的划分region基础上再做些判断。其次是怎么识别tail region的跳走的边。可能是识别region的基础上，看边是不是跳到head和tail的吧。

Interval Analysis as a pre-step?：上面介绍时，似乎说Interval分析是结构分析的预处理步骤。Interval分析可以划分子图，然后子图再去模式匹配。然而观察到，论文里给出的算法居然看不出来有做Interval Analysis。也没有写清楚如何判断一个节点后面的区域是cyclic的，还是acyclic的。这是为什么？

• Acyclic Region：识别是否是IF的三角形，IF-ELSE的菱形。如果不是，就返回匹配失败（归类为proper region）。
• Cyclic Region：识别natural loop。如果无法识别，还是返回失败(归类为improper region)。

可以发现，如果匹配失败，总要用fallback去删边，所以详尽地划分cyclic，acyclic interval也没有意义了，反而是给自己增加了限制，限制必须在这个interval区域内匹配。我们只需要直接匹配过去便是，不必太在于具体是什么region。

natural loop，如果才能

子问题：有向无环图的规约

• 必然存在“叶子节点”，即不指向其他节点的节点。根据这种节点的被指向情况分类
  • 仅有一个节点指向它：类似叶子节点，可以规约成block。
  • 有多个节点指向它：后续寻找菱形，三角形，多分叉合并继续规约。 然而，对于任意子图，并不是都一定能规约成IF-ELSE结构，比如下面的图：

Phoenix 第一个“真正实用”的结构恢复算法

• [Phoenix] 《Native x86 Decompilation Using Semantics-Preserving Structural Analysis and Iterative Control-Flow Structuring》 slides
• reko的实现

paper的3.1节介绍了算法框架，和结构分析很相似。

• 使用后序遍历，遍历每个节点。直观上子节点被处理合并后再处理父节点。遍历每个节点时，判断是acyclic还是cyclic的。
  • 如果是acyclic的区域，算法尝试匹配几种简单的模式，以及潜在的switch语句。匹配不了还是会跳过
  • 如果是cyclic的区域，算法尝试找natural loop，匹配常见的循环模式，或者就是普通的loop。实在处理不了还是跳过
    • 如果匹配失败，进入Loop Refinement阶段（3.6节）。
  • 如果一轮下来都匹配失败了，则使用“最后手段”将一个跳转归类为goto，并忽视它，再重新进行一轮。
    • 优先选择：源节点没有支配目标节点。源节点支配了目标节点的边，大概率是比较重要的边。
    • 优先选择：目标节点支配了源节点。这种不就是natural loop的边吗？

具体应该选择哪些边移除？当前的选择到底好不好？确实是一个值得思考的问题。

Loop的节点：

• 原始的定义：一个反向边的Natural Loop（即，natural loop严格说并不是一个单独的概念，反而是对一条反向边而言的。），是指，最小的，包括反向边头和尾节点的节点集合，集合内所有节点的前驱，要么在集合内，要么这个节点是entry节点，前驱是entry的前驱。
• 存在的问题：不能涵盖一些break语句所在基本块的节点。这些节点被上面定义的“最小”排除。
• 新的定义：除了原始定义中的节点，额外增加了一些节点。
  • 新增节点的定义1：被loop header, 即entry支配的节点中：排除从loop的successor节点，不经过loop header可达的节点。
  • 新增节点的定义2：满足两个条件：条件1：被entry支配。条件2，从loop的successor节点出发，不经过loop header的条件下，不可达。

reko的实现

• Region：算法的主体数据结构，对List<Statement>的封装，但是内部不止可以放指令，还可以放statement。当折叠If, While等结构的时候，它们作为单个statement。
  • 最开始的时候根据基本块的后继块数量情况，每个块创建region，同时将线性的指令都转换为statement。(reko - RegionGraphBuilder)，在算法的迭代下不断折叠。
  • 最后的效果就是整个函数体变成单个linear region。
• Statement：已经结构化的基本块/statement的集合。
  • 不使用Expression，而是结合LLVM的指令。
• LLVM语句序列化写出来就已经可以看作全是goto的高级语言了。因此不额外增加goto statement。

算法的输入输出：首先包括一个将LLVM指令重新折叠为C表达式的数据结构，负责创建所有其他语句。而结构恢复算法，则主要负责创建if，else，while，这些语句。我们基于Clang AST生成C/C++源码。可以发现，clang中有些源码分析也需要CFG，因此也为源码块的CFG数据结构。基于Clang内置的CFG数据结构，我们先将IR转换为这里的CFG结构，然后再由结构分析基于CFG生成完整的文件的AST。

结构化算法尝试将现有的基本块CFG的IR架构，重新组织为类似AST的形式

• 可能会有这种原始的想法：能不能把结果表示为CFG上的简单标记？似乎是不能的，因为是完全不一样的东西。
  • 比如，把结构嵌套折叠到了一个条件跳转里。但是这种折叠，在IR上不一定看得出来。比如，菱形的IF-Then-Else结构，单看IF块就没有明显的从if开头，到整个if结构的successor的边。如果仅把结构分析的结果看作是对边的标记，这里肯定是丢失了信息的。
• LLVM的SSA能否和AST共存？稍微搜了一下，不太能。而且在表达式折叠的时候，遇到这种跨基本块的phi数据流，也适合创建新的变量。

Dream

• Dream:《No More Gotos: Decompilation Using Pattern-Independent Control-Flow Structuring and Semantics-Preserving Transformations》 slides
• fcd decompiler and its blog posts (404 now, find content in web archive)
  • http://zneak.github.io/fcd/2016/02/24/seseloop.html
  • http://zneak.github.io/fcd/2016/02/17/structuring.html
  • http://zneak.github.io/fcd/2016/02/21/csaw-wyvern.html

实现

目标是支持任意IR的转C语言伪代码。一些IR层丢失的类型信息（整数是否有符号，结构体的字段名称等）需要额外的数据结构。

代码优化：Phi指令不好提供支持，我们使用demoteSSA去除Phi指令。为了消除demoteSSA带来的额外空基本块，我们再调用了SimplifyCFG pass。

表达式折叠

副作用的处理：不考虑是否有副作用，即都当有副作用处理。暂时不考虑无副作用的表达式为了简洁的折叠。例如int tmp = 1+2; f(tmp); g(tmp) 不会折叠为f(1+2); g(1+2);

• Stmt和Expr的划分：
  • 如果一个指令没有返回值，纯粹只有副作用，则作为Stmt。例如Store指令。
  • 如果一个指令可能有返回值，则作为Expr，根据引用情况和次数考虑
    • 如果指令没有使用者，则直接将表达式作为stmt插入。
    • 如果指令被基本块外指令引用，或者被当前基本块的指令引用多次，则创建局部变量，然后注册这个局部变量到ExprMap。
    • 如果指令被当前基本块内的指令引用，且仅被引用一次，则直接作为表达式折叠到对应的指令内。直接将当前表达式注册到ExprMap。

Expr现在的表示有bug。Call不好说作为expr还是stmt。并不是有副作用就应该作为Stmt。而是指令没有返回值，不会被作为value才作为Stmt。具体是否应该把Expr作为Stmt放下来，这个都得放。具体是否应该创建一个局部变量，得看是否在一个基本块。如果发现这个Expr的基本块和当前的基本块不同的话，就应该在那边为这个expr创建一个局部变量。

逻辑表达式: C/C++的and/or具有短路的性质。但在无副作用时这影响不大。但是在IR中，如果尝试直接优先折叠成and/or指令，则会不存在短路，语义发生变化。因此逻辑运算符需要在结构分析中处理。

• DemoteSSA会引入不必要的基本块，我们使用SimplifyCFG处理这些基本块。SimplifyCFG同时还会折叠and/or表达式，但是折叠后是select指令的形式。
  • select 指令对应ternary三元运算符。同时select 如果作用在i1，同时两边如果存在false或者true常量时，可以作为and/or处理。
    • select i1 expr1, i1 true, i1 expr2 -> expr1 || expr2
    • select i1 expr1, i1 expr2, i1 false -> expr1 && expr2
• LLVM里的instcombine会将这种模式转为and/or（见这里），但是我们不需要考虑那么多，直接两种都支持。

指令处理

类型

• 将IR类型对应地带着指针类型转换，冗余的解引用和取地址~~使用窥孔优化~~在生成AST时消除：IR的全局变量对应它的指针类型，alloca对应局部变量的指针类型。
  • 窥孔优化：clang没有自带的。根据ASTMatcher自己写一个吧。 根据这里，AST其实很难修改。
    • Clang::Tooling::transformer：将AST修改为对应的代码文本。通过再次parse，有可能可以实现类似AST修改的效果。
    • lib/Sema/TreeTransform.h内部库。没有细看。
    • clangTooling, rewriter: 例如这里, 在AST转文本代码的时候介入并进行修改。

名称

为了简化设计，全局不允许出现重名的情况。全局使用IdentifierInfo判断重名情况，重名时尝试增加"_1"递增的数字后缀。函数内使用Names判断重名情况

• 尽量还原LLVM IR，使用IR中的名称
  • GlobalVariable，Function等使用IR对应的名称。
  • 局部变量对应alloca指令，因此使用Alloca指令的名称。
  • 如果没有名称，则生成前缀加编号的临时名称，如func_1。

ConstantExpression

• 常量数组，常量结构体
  • 直接的对应是Compound literals再内置InitListExpr。但它会创建一个匿名对象，所以大部分情况还是不会转成它的。
    • 如果是在初始化变量，则直接转换成纯InitListExpr。
    • （暂未实现）如果在其他地方（如指令里）用到了，同时是递归的最外层，则
      • 结构体转换成ImplicitCastExpr(LValueToRValue) + Compound Literal + InitListExpr。
      • 数组转换成ImplicitCastExpr(ArrayToPointerDecay) + CompoundLiteralExpr(array) + InitListExpr。
    • 如果是递归创建内部的表达式，则只创建InitListExpr部分。
  • 如果遇到了ConstantInitializerZero，则应该转换为InitListExpr + array_filler: ImplicitValueInitExpr
  • 创建常量需要传入一个额外的类型：
    • 创建ImplicitValueInitExpr需要设置类型。
    • 创建Compound Literal也需要类型。
• 结构体类型
  • LLVM中预定义的结构体类型，提前遍历并存放好。维护一个从llvm type到RecordDecl的映射。
  • LLVM中的Literal 结构体转换为C语言中的匿名结构体。
    • 首先看当前llvm Type是否被映射和缓存，即该匿名结构体已经遇到过。
    • 直接创建一个匿名RecordDecl，加入映射，并直接插入到TranslationUnitDecl里的当前位置。
  • 结构体成员名字无法保存在IR中。（TODO，目前直接按顺序生成一个名字）
    • 结构体的成员名字可以考虑保存在Meta data，如DebugInfo里
    • 缺点：必须依附于这个类型的全局变量。不能直接依附到类型上。MataData只能依附于指令，函数等

BinaryOperator

• 加法：nsw，nuw。当溢出时会变成poison value。这个暂时不考虑。
• 移位运算：逻辑移位对应C语言无符号数字的移位，算数移位对应有符号数字的移位。（根据这里）

运算符优先级：Operator Precedence

C Operator Precedence

总体的优先级顺序：变量成员和数组访问和后缀一元运算符，前缀一元运算符，其他二元运算符。注意：

• 变量成员和数组访问其实可以看作是一种后缀一元运算符。Clang里这两者是单独的表达式类型。既然它们优先级最高，就不需要单独考虑处理。函数调用，强制类型转换同理。
• 一元运算符根据前缀和后缀分两个优先级。
• 三元运算符，中间可以看作已经带了括号，从而看作一个二元运算符。

增加函数考虑是否增加括号：

• 函数1：获取表达式优先级
  • 判断是一元，二元，三元，然后给出优先级数字值。
• 函数2：根据优先级获取结合律，返回bool类型，是左结合还是右结合
• 函数3：参数1 当前运算符优先级，参数2 子表达式优先级，参数3: bool is_left 运算符左边还是右边
  • 判断子表达式优先级是否低于当前一元运算符优先级，是则增加括号。
  • 如果优先级同级，调用函数2获取结合律信息，然后根据左结合和右结合处理。左结合运算符：如果同级则不需要在左边子表达式增加括号。
    • 如果结合率和当前处理的边相同则不需要括号，反之需要括号。

CallInst

• Organize and maintain a map from llvm functions to Clang function declarations.
• Handle function pointers: TODO

Alloca指令

根据alloca指令是否在函数开头的必经之路（从entry遍历找到只有一个succ和pred的集合）上，将alloca分为动态alloca和静态alloca。

• 静态Alloca：创建对应类型的变量。

• 动态Alloca（很少）：TODO，转换为alloca函数调用

• AllocaInst:

  • If the inst is at the outermost level, then create a corresponding local variable.
  • If not, this is a rare case, create corresponding calls to the alloca function.

GetElementPtr

LLVM数组与C数组的对应：

• C数组变量 -> LLVM数组指针再解引用一下（LLVM常通过指针操作变量）
• gep操作时第一个index不为0 -> C里面int arr[3]; (&arr) + 1 （意味着GEP不需要在开头默认解引用一下）
• gep如果有且只有第一个index，则类型不变 -> GEP结束隐含了取地址操作。

GEP中途每一步结束并没有保证结果是指针类型，而是在结束的时候额外做了取地址。 GEP每一步类型必定会细化：如果是指针，则会解引用（数组取成员0），如果是数组或者结构体，会取成员。

C的指针相关运算内部细节：

• 结构体运算：结构体值 -> 结构体成员值
  • 箭头运算：结构体指针 -> 结构体成员值 （在开始前先解引用）（对应Gep里的两步）
• 数组运算：
  • 数组值到数组成员值
  • 指针的数组运算（不考虑）：指针到指针解引用后成员值（指针运算外加解引用）（对应Gep里的两步）
    • 解引用运算 = 数组下标取0
• 指针加减法运算：指针值 -> 新指针值
• 解引用运算 + 取地址
  • 指针 -> 指针内部成员指针

GetElementPtr先获取内部指针值的类型，然后依次处理每个下标：

• 如果是结构体成员或者数组，则先解引用，然后增加运算，然后再取地址。

添加注释

添加注释不是简单地插入AST，因为Clang没有把注释这样管理，而是直接插入到ASTContext里面，而且要创建RawComment，而不是对应的语法树结构。没有找到将对应的Comment类插入进去的函数，应该需要自己实现。可能需要把字符串直接插入SourceManager里面，然后把sourceRange拿出来创建Comments。

现有论文与资源

资源集

Working Conference on Reverse Engineering (WCRE)：

PPREW-5: Proceedings of the 5th Program Protection and Reverse Engineering Workshop 这个期刊好啊。

SSPREW: Software Security, Protection, and Reverse Engineering Workshop

其他：

• RetDec的publication
• Decompiler Design - Type Analysis 居然有介绍反编译器架构的网站。

Github的两个list：

• Awesome-Info-Inferring-Binary
• Awesome-Binary-Rewriting

课程

• CMU Lecture Notes on Decompilation (15411: Compiler Design) 反编译内部各个阶段都有介绍。

现有的反编译器

1. Ghidra ghidra/docmain.hh at master · NationalSecurityAgency/ghidra (github.com) 看代码前构建doxygen看文档。
2. avast/retdec: RetDec is a retargetable machine-code decompiler based on LLVM. (github.com)
3. Boomerang Decompiler (sourceforge.net) BoomerangDecompiler/boomerang: Boomerang Decompiler - Fighting the code-rot :) (github.com)
4. yegord/snowman: Snowman decompiler (github.com)
5. angr好像也有了

读论文

反编译器中端很好的资料：Static Single Assignment for Decompilation (Boomerang) 感觉可以抓住优化方面的脉络。虽然还是有不少启发式的方法，但相比其他资料已经好了很多。SSA现在也已经是反编译器不可缺少的重要部分。

控制流结构恢复-structural analysis

很多都是借用现有的type recovery，重点去讲structure recovery。

• 【Phoenix】 《Native x86 Decompilation Using Semantics-Preserving Structural Analysis and Iterative Control-Flow Structuring》 slides

  Edward Schwartz's PhD thesis 里面进一步介绍了Phoenix反编译器

  在reko反编译器里也有这个算法的实现

  这篇论文关注控制结构的恢复。控制结构的恢复最早是基于interval analysis的（？这是什么得学一学）。后面才被细化为structural analysis。

• 【Dream】No More Gotos: Decompilation Using Pattern-Independent Control-Flow Structuring and Semantics-Preserving Transformations slides code

• 【Rev.ng】A Comb for Decompiled C Code Rev.ng他们2020年的新的反编译的结构恢复算法。

类型恢复 - Type Recovery

• 【TIE】Principled Reverse Engineering of Types in Binary Programs. 这篇基于VSA搞了自己的DVSA，主要区别是StridedInterval里可以放除esp外的变量符号？。重点主要在后面的约束求解部分。后面的类型系统和求解部分也非常复杂TODO。

• 【DIVINE】: DIscovering Variables IN Executables 这篇还是VSA系列的那些人写的。讲先用最简单的semi naive方法鉴别变量，跑VSA，然后拿VSA结果去生成约束跑ASI。迭代几次得到最好的结果。 里面说如果变量是8字节大小，那VSA直接无法处理，值总是Top（32位程序）。那就不能直接把内存最大切分粒度搞成4字节？？

• 【REWARDS】Automatic Reverse Engineering of Data Structures from Binary Execution TODO

• 【retypd】 需要进一步学习类型系统的高级知识，比如subtyping。它不仅开源，而且不需要VSA的指针信息。可以与之前需要VSA的结合？但是似乎没有说怎么从一整块栈内存中识别出变量。

• 【SecondWrite】Scalable Variable and Data Type Detection in a Binary Rewriter

变量恢复

变量恢复和类型恢复关联较大。如果把函数开头分配的栈空间看作一个巨大的结构体，变量恢复就转换成了类型恢复。

OSPREY: Recovery of Variable and Data Structure via Probabilistic Analysis for Stripped Binary slides 把变量的访问看作变量存在的暗示，同时存在很多这样的暗示，使用概率性的推导。好像是基于后面那篇BDA的工作。

C++ 反编译

C++的类给反编译带来了额外的困难，涉及到（复杂的）约束求解等。

• OOAnalyzer: Using Logic Programming to Recover C++ Classes C++反编译 and Methods from Compiled Executables

• SmartDec: Approaching C++ Decompilation.

• Reconstruction of Class Hierarchies for Decompilation of C++ Programs.

VSA相关

• WYSINWYX: WHAT YOU SEE IS NOT WHAT YOU EXECUTE 第三章讲了VSA的事情。它也讲了很多二进制分析的事情。

  ■ 文中提到的一些其他的没有用到VSA的方法：

  [33] C. Cifuentes and A. Fraboulet. Interprocedural data flow recovery of high-level language code from assembly. Technical Report 421, Univ. Queensland, 1997.

  [34] C. Cifuentes and A. Fraboulet. Intraprocedural static slicing of binary executables. In Proc. Int. Conf. on Software Maintenance (ICSM), pages 188–195, 1997.

  [35] C. Cifuentes, D. Simon, and A. Fraboulet. Assembly to high-level language translation. In Proc. Int. Conf. on Software Maintenance (ICSM), pages 228–237, 1998.

  [45] S.K. Debray, R. Muth, and M. Weippert. Alias analysis of executable code. In Proc. Principles of Programming Languages (POPL), pages 12–24, January 1998.

• 基础的VSA Analyzing Memory Accesses in x86 Executables

• Improved Memory-Access Analysis for x86 Executables GMOD-Based Merge Function

  这篇论文开头有很多引用：Research carried out during the last decade by our research group [64, 65, 6, 56, 55, 7, 8, 36, 4, 49, 9] as well as by others [48, 22, 33, 14, 2, 31, 13, 44, 32, 3, 54, 37, 21, 46, 28, 19, 16, 34, 66] has developed the foundations for performing static analysis at the machine-code level. 能找到非常多的其他paper了？

  没想到相比于源码级的分析，二进制级的分析还有好处。有很多源码层没有指明的实现细节（比如C++的表达式求值顺序），源码级分析想要sound需要考虑所有可能的实现，而二进制级的分析只需要考虑编译器选择的实现。

• 《DIVINE: DIscovering Variables IN Executables》 （VSA with ASI(Automated Struct Identification)）（栈变量恢复）VSA可以用于一定程度的变量恢复。

• 这人想要实现Value Set Analysis到RadecoIL上。

• 这里 也有人实现，还有WYSINWYNX那个论文相关的东西？

• 这个课件讲到了一点点。这门课是和安全相关的。TODO，不太看得懂。

框架与综述

• C Decompilation : Is It Possible? 2009的一篇

  第二章相关工作里面有不少引用：

  structural analysis：[4–6]，这个也用在了编译器：[8]。

  unification-based algorithm for recovery of types：Mycroft [9]

  现有反编译器：DCC decompiler [7]. Boomerang [11], REC [12] and Hex-Rays plug-in [13]

• 【rev.ng】rev.ng: A Multi-Architecture Framework for Reverse Engineering and Vulnerability Discovery.

  这个反编译器开源了lifter：先转到Qemu IR然后转到LLVM IR。这个好像也不太和反编译相关，也只是搞插桩、fuzzing的。

下游研究

• Augmenting Decompiler Output with Learned Variable Names and Types 基于AI恢复反编译的变量名。

反编译器测试

• 【DecFuzzer】How far we have come: testing decompilation correctness of C decompilers 代码

  functionality-preserving disassembling and C style control structure recovery [17, 31, 47, 64, 65, 67]

  变量恢复static analysis and inference techniques [10, 12, 13, 30, 54].

  fool-proof techniques for binary disassembling and decompilation [17, 31, 64-67].

  EMI编译器测试看了下是插入了不影响语义的代码之后去开编译优化，发现优化器做出的错误决定而导致的crash。比如把一个不该执行的循环内操作提到外面。错误判断一些分支恒为真或假。是设置Csmith的输出使得只生成一个函数？？

  本来Csmith生成的代码很多全局变量的使用。如果全局变量改变了，很难手动找到是哪个函数？它是生成了局部变量，然后把对全局变量的使用全替换成了局部变量，函数结束的时候把局部变量的值update到全局变量，这样如果全局变量变了，就肯定是在最后update的时候改变的。那手动看的时候不要继续找内部怎么使用？这样做有什么好处吗。。。可能是方便找到这个函数到底涉及到了哪些全局变量，然后方便只提取这些到反编译结果的全局变量？？

• Semantic Fidelity of Decompilers CMU的技术报告。这篇基于上面的进一步做了。基于副作用（全局变量，内存访问，函数调用）分析单个函数函数的反编译正确性。

SecondWrite系列

• Decompilation to Compiler High IR in a binary rewriter 提升到编译器IR，然后优化。对写反编译有较大启发

  • 有一段提到了栈编译的坏处。

基于搜索的反编译

• Evolving Exact Decompilation 好像和主流的反编译技术不同。
• Decompilation as search

Java 字节码反编译

Java反编译的几篇

• Proebsting and Watterson [24] 《Krakatoa: Decompilation in java (does bytecode reveal source?).》
• Dava Miecznikowski and Hendren [22] 《Decompiling java bytecode: Problems, traps and pitfalls》
• Naeem and Hendren [25] 《Programmer-friendly decompiled java,》
• Harrand et al. [27] present Arlecchino 《Java decompiler diversity and its application to meta-decompilation》
• 《Decompiler Implementation》 一本书，讲Java字节码反编译的，暂未找到免费的电子版。

其他相关的静态分析技术

Aggregate structure identification and its application to program analysis

其他

• Decomperson: How Humans Decompile and What We Can Learn From It 人经常会看生成的汇编，做些很小的修改。意味着可能可以强化学习。另外反编译可能代码片段可以拆分成子任务？，因为人经常关注一个小片段。

• A Survey of Software Reverse Engineering Applications | SpringerLink 讲了逆向软件分析的合理性，用处等等。以后写intro的时候很有用。

• An evaluation of output from current Java bytecode decompilers: Is it Android which is responsible for such quality boost?

• Retrofitting Security in COTS Software with Binary Rewriting 给二进制增加保护。也提到了优化

• DECOMPERSON: How Humans Decompile and What We Can Learn From It 调研人工反编译的过程

• 研究VSA对人工分析的帮助。（对学习VSA没啥用）

最近的新论文

• DEEPVSA: Facilitating Value-set Analysis with Deep Learning for Postmortem Program Analysis 这篇参考意义不大，是ML结合的。

• BDA: Practical Dependence Analysis for Binary Executables by Unbiased Whole-Program Path Sampling and Per-Path Abstract Interpretation

• BinPointer: Towards Precise, Sound, and Scalable Binary-Level Pointer Analysis

  提及：BPA: Refining Indirect Call Targets at the Binary Level这篇也值得读。用了块内存的抽象解释。

Existing projects

• reko A decompiler with GUI, still actively maintained.

• decomp 2020, an attempt to decompile using LLVM IR to golang. and a list of other decompiler

• github.com/repzret/dagger 反编译到LLVM IR。aarch64还在开发过程中。介绍的slides

• avast/retdec

• Boomerang (sourceforge) or BoomerangDecompiler/boomerang (github.com)

• yegord/snowman (github.com)

• angr好像也有了反编译

其他资料（网页等）：

• https://github.com/cmu-sei/pharos 涉及到很多反编译技术

• https://news.ycombinator.com/item?id=11218138 两个人的讨论。里面推荐对两篇文章的逆向引用搜索：https://scholar.google.com/scholar?as_ylo=2018&hl=en&as_sdt=2005&sciodt=0,5&cites=1148004013363547510&scipsc= https://scholar.google.com/scholar?cites=7322807636381891759&as_sdt=2005&sciodt=0,5&hl=en

• https://github.com/toor-de-force/Ghidra-to-LLVM https://uwspace.uwaterloo.ca/bitstream/handle/10012/17976/Toor_Tejvinder.pdf?sequence=3&isAllowed=y Ghidra Pcode编译到IR。代码太简单了。。栈内存好像是alloca出来的，可能还是想保持语义想运行。

• https://github.com/decomp/decomp 这人也想基于LLVM IR然后去优化。https://github.com/decomp/doc 相关文档

• The Decompilation Wiki.

  dagger主要讲的是反编译到IR上，找到语义等价的LLVM IR的指令的过程。感觉有点像编译器后端的Instruction Selection，可能能用上利用DAG（有向无环图）选择指令的技术。它是作为llvm的fork编写的，2017后就没有维护了。和llvm耦合好严重啊，都不知道哪里是它的代码。好像好复杂。

• https://github.com/JuliaComputingOSS/llvm-cbe 曾经IR到C有一个backend，2016年被移除了。现在有人接手

• https://corescholar.libraries.wright.edu/cgi/viewcontent.cgi?article=3277&context=etd_all LLVM IR based decompilation。

• https://github.com/lifting-bits/sleigh sleigh作为Ghidra的反编译器，是用C++写的，而且汇编到pcode的lift部分也是它负责的。所以用Ghidra可能也只要用这个就可以了。

• Ghidra上的ASI https://blog.grimm-co.com/2020/11/automated-struct-identification-with.html

领域的研究者

Edward Schwartz

Shuai Wang

Gang Tan

WebAssembly

University of Stuttgart 的 Michael Pradel 以及他的学生 Daniel Lehmann 在webassembly方面发了很多paper。

WebAssembly的反编译

一篇本科毕业论文《Decompilation of WebAssembly using Datalog》，可以在这里下载到全文。作者是LOVE BRANDEFELT，代码在这个gitlab仓库

基于Rust语言，遍历了各种指令，导出为Facts，代码并不复杂。Facts包含大量的CSV文件。

Ghidra

资源

其他资源列表：

• Ghidra - low level 这里有很多其他资源，dump local variables的脚本。和搭建调试环境的issue链接。
• Awesome Ghidra

书籍：

• 《THE GHIDRA BOOK The Definitive Guide》 TheGhidraBook.pdf
• 《Ghidra Software Reverse Engineering for Beginners》 有pdf

使用教程：

• Ghidra API的tutorial：https://github.com/HackOvert/GhidraSnippets
• Dump出high-pcode的教程 https://github.com/HackOvert/GhidraSnippets#dumping-refined-pcode
• 基于Ghidra实现的VSA：https://github.com/penhoi/ghidra-decompiler/wiki/Symbolic-Value-Set-Analysis
• 如何开发调试Ghidra：https://spinsel.dev/2021/04/02/ghidra-decompiler-debugging.html 这人也

代码分析：

• 《Ghidra To The Next Level》 丁湛钊的介绍 这个slides讲了不少ghidra的反编译器的设计。
• 《记一次对Ghidra反编译的修复》解释了反编译原理，里面解决的问题其实就是栈变量识别相关的
• DevGuide.md 官方的eclipse环境搭建
• 《Exploring Ghidra’s decompiler internals to make automatic P-Code analysis scripts》解释了一些decomp_dbg的代码。

Ghidra-sleigh 调试环境搭建

相关的C/C++代码主要在 Ghidra/Features/Decompiler/src/decompile.cpp下。docmain.hh和 doccore.hh两个文件可以先看，或者先build doc出来，生成的doc在../doc目录（Ghidra/Features/Decompiler/src/decompile/doc/html/index.html）

Ghidra-sleigh的ghidra/docmain.hh 里有很多文档，看代码前构建doxygen看文档。

根据这里https://daniao.ws/notes/quick-tips/build-ghidra 下载并编译Ghidra。生成各种中间文件

sudo apt install openjdk-17-jdk-headless unzip --no-install-recommends
wget -c https://services.gradle.org/distributions/gradle-8.1.1-bin.zip -P /tmp
sudo unzip -d /opt/gradle /tmp/gradle-8.1.1-bin.zip
export PATH=$PATH:/opt/gradle/gradle-8.1.1/bin
echo 'export PATH=$PATH:/opt/gradle/gradle-8.1.1/bin' >> ~/.bashrc

git clone https://github.com/NationalSecurityAgency/ghidra.git
git checkout Ghidra_10.3.1_build
git checkout -b mydev
gradle --init-script gradle/support/fetchDependencies.gradle init
gradle buildGhidra

然后vscode打开文件夹/home/ubuntu/ghidra/Ghidra/Features/Decompiler/src/decompile

使用bear生成compile_commands.json文件

bear -- make decomp_dbg

增加debug配置。注意里面的环境变量指向ghidra源码文件夹

{
    "version": "0.2.0",
    "configurations": [
        {
            "type": "lldb",
            "request": "launch",
            "name": "Debug",
            "program": "${workspaceFolder}/cpp/decomp_dbg",
            "args": [],
            "cwd": "${workspaceFolder}/datatests",
            "env": {"SLEIGHHOME": "/home/ubuntu/ghidra"}
        }
    ]
}

从ghidra图形界面，反编译的右上角的debug decompiler里面可以导出xml文件，用于调试。

调试与decomp_dbg常用命令

https://github.com/NationalSecurityAgency/ghidra/issues/720

load file test 加载二进制文件
load addr 0x1149
decompile
print C

restore Reset.xml    加载xml文件
trace address
trace list

搜索相关的命令：registerCommands registerCom

部分命令需要OPACTION_DEBUG开启

反编译器代码解读（sleigh）

总体分析流程

Ghidra的Java部分代码启动sleigh子进程，然后通过stdin输入xml文件，stdout读取xml文件作为反编译结果。比如Ghidra\Features\Decompiler\src\main\java\ghidra\app\decompiler\DecompileResults.java parseRawString函数这里开始解析反编译器的输出的。Ghidra\Framework\SoftwareModeling\src\main\java\ghidra\program\model\pcode\HighFunction.java readXML函数里可以看到high pcode是基于这个ast的标签解析的。

反编译输出展示上面的选项里，选Debug Function Decompilation导出的xml文件是反编译器的输入。根据https://github.com/NationalSecurityAgency/ghidra/issues/720 这里可以使用decomp_dbg命令行输入xml文件进行反编译。

应该反编译过程中，Pcode都是一套Pcode，只不过https://spinsel.dev/assets/2020-06-17-ghidra-brainfuck-processor-1/ghidra_docs/language_spec/html/additionalpcode.html 有一些额外的东西只有在反编译之后才会产生。

反编译阶段

首先反编译过程被分为了几个大的 simplification styles Root Action Groups。它们由 base groups （例如 “stackvars” or “typerecovery”） 组成。

• decompile – The main decompiler action
• normalize – Decompilation tuned for normalization
• jumptable – Simplify just enough to recover a jump-table
• paramid – Simplify enough to recover function parameters
• register – Perform one analysis pass on registers, without stack variables
• firstpass – Construct the initial raw syntax tree, with no simplification

在universalAction函数里构建了所有可能的Action和Rule列表，即定义了他们的执行顺序。每个Action或Rule是否运行再由标签确定。

Rule: 代表着某个特定的点位可能采取的操作。它输入一个Pcode位置，首先判断能不能在该处应用，然后再应用更改。Rule可以通过getOpList()函数先给出一个点位可能的Opcode列表，方便外部提前过滤。多个Rule可以组合为ActionPool

Action 类似Pass，对一个函数做变换。每次变换递增一下count变量。

和栈分析相关的标签：localrecovery typerecovery stackvars

和栈分析相关的标签，和内部的Action和Rule：

base

• ActionHeritage SSA构建算法。

localrecovery - ActionRestrictLocal: 限制局部变量在栈上的可能范围，排除一些参数之类的栈范围，使得这些范围不会创建局部变量。 - 首先对每个FunctionCallSpecs，的每一个参数，把它们的地址排除在局部变量之外。 - 对保存的caller的寄存器，相关的栈内存排除在局部变量之外。 - 注：可见wasm里不用管这些。 - ActionRestructureVarnode - gatherVarnodes：从varnode中收集栈上值的类型信息。它遍历funcdata在stack这个space上的Varnode，然后在对应的栈偏移处增加当前varnode的类型信息，表示为增加一个RangeHint - gatherOpen：先调用 AliasChecker::gather，收集一个AddBase的list，包含所有的栈相关指针，然后对每个指针调用gatherOffset, 收集偏移。最后会设置一个aliasBoundary为最小的offset，可能比它大就可能alias。 - AliasChecker::gather：对于给定的函数和address space（栈），收集所有，指向当前地址空间的，指针（varnode）。 - AliasChecker::gatherAdditiveBase：首先从栈指针开始，收集所有和它有关的加法操作（INT_ADD, INT_SUB, PTRADD, PTRSUB, and SEGMENTOP）。广度优先地遍历，vnqueue作为worklist。最后生成了AddBase的一个list，表示每个有关的root varnode和可能存在的index varnode。 - gatherOffset：对每个收集的AddBase的base调用，负责计算出varnode的常量offset - gatherSymbols： - ScopeLocal::restructure：

stackvars - RuleLoadVarnode - RuleStoreVarnode

stackptrflow - ActionStackPtrFlow - checkClog: Clog是指，栈指针加栈上的值？ - analyzeExtraPop: sub-functions TODO，难道是说子函数里面用父函数栈指针？

decomp_dbg 代码位于consolemain.cc（main 函数，也定义了 load/save/restore几条命令）、ifacedecomp.hh/cc （反编译相关命令）。

• Heritage::discoverIndexedStackPointers

通过一通搜索，我找到了restructure varnode这个action，发现了一些问题。这个action的主要工作就是调用 ScopeLocal::restructureVarnode函数（varmap.hh/cc)，这个函数的工作分配给了 MapState::gatherVarnodes 、MapState::gatherOpen 和 MapState::gatherSymbols ，最后调用了ScopeLocal::restructure。

其中有关的部分在gatherOpen和gatherVarnodes。gatherOpen在正常情况下，应该分析出好几段栈空间对应的 open RangeHint ，其中的处理逻辑在AliasChecker::gather -> AliasChecker::gatherInternal -> AliasChecker::gatherAdditiveBase 。

MapState::gatherVarnodes

所以，我将范围扩大到在heritage 、restructureVarnodes action之后，然后找到了相关的action ：RuleLoadVarnode和 RuleStoreVarnode。

这两个action（其实是Rule）应该就是分析的主要了，他们都会经过RuleLoadVarnode::checkSpacebase -> RuleLoadVarnode::vnSpacebase -> RuleLoadVarnode::correctSpacebase (ruleaction.cc) 的检查。调试发现，没能分析出来的变量所对应的 store/load在correctSpacebase的检查中失败了 。

这两个action（其实是Rule）应该就是分析的主要了，他们都会经过RuleLoadVarnode::checkSpacebase -> RuleLoadVarnode::vnSpacebase -> RuleLoadVarnode::correctSpacebase (ruleaction.cc) 的检查。调试发现，没能分析出来的变量所对应的 store/load在correctSpacebase的检查中失败了。

ActionDatabase::buildDefaultGroups 分析好像是分组的，里面很多rule。

“simplification styles” are also referred to as “root actions” or “groups” in the decompiler source code. They consist of groups of “base groups” such as “stackvars” or “typerecovery”, which are more fine-grained groups of specific analysis operations.

Ghidra 中的 value set analysis

• ValueSetSolver VSA分析。好像会先执行vsSolver.establishValueSets给要分析的值赋初始值，然后调用vsSolver.solve运算。
  • CircleRange: 底层抽象域，针对不同opcode写了运算，例如CircleRange::pushForwardBinary负责binary op
  • 使用方面，有两个使用点：一个IfcAnalyzeRange好像是执行analyze range full|partial <varnode>命令的时候触发。另外一个是ValueSetSolver.analyzeNewLoadGuards函数，为LoadGuard确认访问范围。
• LoadGuard: 对一个，访问了栈，但是是在动态访问栈的load指令的描述。描述其可能访问的栈范围。包括min, max, step等。和VSA分析有很大关系。

编写插件

Ghidra scripting

• 命令行直接加载二进制文件，可以设置分析后是否保存 https://static.grumpycoder.net/pixel/support/analyzeHeadlessREADME.html#scripting_headlessScripts_controlProgramDisposition

• 如何遍历定义的结构体成员 https://reverseengineering.stackexchange.com/questions/21320/automate-looking-for-calls-to-an-offset-of-a-structure

  structure.getDefinedComponents Ghidra\Framework\SoftwareModeling\src\main\java\ghidra\program\model\data\CompositeInternal.java 的dumpComponents方法是结构体转string的时候用到的。

• 获取创建符号 getSymbols(name, namespace)

• 获取和创建函数 FlatAPI的getFunction系列。按照namespace获取函数是在listing里：getCurrentProgram().getListing()

  Flatapi的createFunction。更多创建函数在FunctionManager：getCurrentProgram().getFunctionManager().createFunction

  getCurrentProgram().getExternalManager().addExtFunction好像同时会创建External Location和对应的函数？

• 指定地址寻找函数 看了下flat program api里面对getFirstFunction和getFunctionAfter的实现，发现就是currentProgram.getListing().getFunctions函数的简单调用。而且getFunctionAfter还有传入地址和函数的版本。

• 设置函数签名 FunctionSignatureParser负责的就是修改函数的时候，上面那个输入框的解析。

  FunctionEditorModel这个类负责这个输入框背后的逻辑：调用上述parser，得到FunctionDefinitionDataType，然后调用自身的setFunctionData函数。函数内部设置函数的参数和返回值。

• 偏移找寄存器 \ghidra_10.1.2_PUBLIC\Ghidra\Processors\ARM\data\languages\ARM.sinc看这个文件

• 设置/读取寄存器值 https://ghidra.re/ghidra_docs/api/ghidra/program/model/listing/ProgramContext.html

  program.getProgramContext().setValue(register, start, end, value); 一般可以start=end=想要的地址

  Ghidra\Features\Base\src\main\java\ghidra\app\util\viewer\field\RegisterFieldFactory.java getRegisterStrings好像是负责写assume xxx = xxx的。

  Ghidra\Features\Base\src\main\java\ghidra\app\util\viewer\field\RegisterFieldFactory.java getSetRegisters负责获取设置的寄存器

• 加载头文件报错的常见解决方法 在parse C source界面之所以会标红，应该是要自己在下面的-I选项给出这些头文件存在的位置。比如我的-IC:\Program Files\LLVM\lib\clang\13.0.0\include

  -IC:\Program Files (x86)\Dev-Cpp\MinGW64\lib\gcc\x86_64-w64-mingw32\4.9.2\include

  目前用到size_t的还真的不知道怎么办。上面两个头文件处理后都不太行，变成typedef SIZE_TYPE size_t;这种，而且完全看不到int32_t的定义。所以windows下的头文件不太行。还是得看看。最后从wsl里复制header出来，在x86_64-linux-gnu\bits\types.h这里定义了。但是我include好像没用，不知道为什么

  TODO：暂时放弃，直接使用types里面复制处理的。

  #define __stdcall
  struct va_list; // shitty hack
  typedef struct va_list *va_list;
  
  typedef long int ptrdiff_t;
  typedef long unsigned int size_t;
  

  有些可以直接用-D参数的方式解决。-D甚至可以定义函数式宏：https://stackoverflow.com/questions/31857559/gcc-define-function-like-macros-using-d-argument

  -D__attribute__(x)= 好像没有用，但是ghidra好像能直接识别，不会报这个的错

  -Dsize_t="unsigned long"
  
  /* Fixed-size types, underlying types depend on word size and compiler.  */
  typedef signed char __int8_t;
  typedef unsigned char __uint8_t;
  typedef signed short int __int16_t;
  typedef unsigned short int __uint16_t;
  typedef signed int __int32_t;
  typedef unsigned int __uint32_t;
  #if __WORDSIZE == 64
  typedef signed long int __int64_t;
  typedef unsigned long int __uint64_t;
  #else
  __extension__ typedef signed long long int __int64_t;
  __extension__ typedef unsigned long long int __uint64_t;
  #endif
  

MemoryBlock

原来没有直接的方法，是通过创建新Block然后调用join方法。

Ghidra\Features\Base\src\main\java\ghidra\app\plugin\core\memory\ExpandBlockModel.java applyTo函数

• 读写内存区域 Uninitialized的内存默认是不能写的，需要把要写的部分分割开，然后设置成initialized。

  https://github.com/NationalSecurityAgency/ghidra/issues/3585

• 动态链接与Thunk Function

  ThunkFunction corresponds to a fragment of code which simply passes control to a destination function. All Function behaviors are mapped through to the current destination function. 另外thunk不需要设置参数和返回值类型，直接复制的目标对象的类型。

  主要的逻辑在Ghidra\Features\Base\src\main\java\ghidra\app\util\opinion\ElfProgramBuilder.java这里。当加载程序的时候，它会处理各种符号。单是创建单独的external符号是在“”（Library.UNKNOWN）这个库下的，默认没有map到内存中，所以getExternalSpaceAddress这里是一种Fake的地址。而内存中的“EXTERNAL”（MemoryBlock.EXTERNAL_BLOCK_NAME）是ElfProgramBuilder创建的。（通过搜索NOTE: This block is artificial and is used to make relocations work correctly找到的）

  为什么他创建的thunk方法可以不在listring的Function里显示，秘诀大概是：getCurrentProgram().getSymbolTable().removeSymbolSpecial。参照下面文件里搜索removeSymbolSpecial的代码。

  分配单独的一块内存创建EXTERNAL块相关的逻辑在Ghidra\Features\Base\src\main\java\ghidra\app\util\opinion\ElfProgramBuilder.java allocateLinkageBlock函数。

查看high p-code

https://reverseengineering.stackexchange.com/questions/29646/dump-pcode-in-ghidra-for-a-specific-decompiled-function 直接在界面点就可以，但是好像只是为了给你看形状的。打开python然后currentLocation.token.pcodeOp也可以稍微看看当前指针位置的。

RetDec

• retdec/publications at master · avast/retdec (github.com)
  • 综述：Retargetable Analysis of Machine Code

代码

https://zhuanlan.zhihu.com/p/509763117 有一些源码解读的内容。

• retdec的4.0是最后一个包含单独的ir转c工具的版本。相关代码src/llvmir2hlltool/CMakeLists.txt (要先checkout到v4.0。)

开发环境

在cmake配置里增加"-DCMAKE_INSTALL_PREFIX=/home/xx/retdec/build/retdec-install"，然后直接使用cmake插件，目标选择install。（因为retdec-decompile工具需要找到decompiler-config.json文件，因此需要安装）

在deps/llvm/CMakeLists.txt里面将LLVM的构建设置为RelWithDebInfo，后续调试的时候能够看到更多的内容，比如LLVM的结构体成员的内容。

可以使用Vscode + cmake 插件，在设置里为cmake配置额外的参数，设置安装的前缀路径即可。

"cmake.configureArgs": [
    "-DCMAKE_INSTALL_PREFIX=/sn640/retdec/build/retdec-install"
],

入口

• retdec-decompiler.cpp 主要是解压，脱壳什么的，然后调用retdec::decompile函数。这里的retdec是namespace，不是class，所以就在src/retdec/retdec.cpp。
• 其中非常重要的是读取share/retdec/decompiler-config.json，其中有llvmPasses这一项，指定了一系列pass名字。然后在那边retdec::decompile函数，他会根据config.parameters.llvmPasses里的值找到pass，然后依次加入passmanager里。然后pm.run(*module);运行结束之后，一切反编译过程都完成了。

Pass

基于src/retdec-decompiler/decompiler-config.json列出来的每个pass名字，对每个pass的名字带双引号（比如"retdec-decoder"）在vscode里搜索，可以直接定位到对应的Pass代码位置。

• retdec-provider-init： 这个pass负责给很多Provider类设置信息（到静态变量里）。FileImageProvider，DebugFormatProvider，DemanglerProvider等等。如果我们要设置一下简单的，可以直接在Pass运行前加。
• retdec-decoder：src/bin2llvmir/optimizations/decoder/decoder.cpp 负责把capstone的结果转成IR。
• "retdec-x86-addr-spaces"：把一些对FS，GS寄存器寻址的访问转成intrinsic call，如getReadFsByte
• retdec-x87-fpu: replace fpu stack operations with FPU registers
• retdec-main-detection: 识别出main函数之后，也就是（在retdec自己的config里）重命名了一下。
• retdec-idioms-libgcc：把一些libgcc的算数运算替换成LLVM里的运算。
• retdec-idioms：把常见的指令组合替换成别的指令？
• retdec-inst-opt：好像是简单的窥孔优化。
• retdec-inst-opt-rda：
• retdec-cond-branch-opt 这些优化应该不用
• retdec-syscalls：好像是把系统调用转成对应的call？有一个map
• **retdec-stack：**关键Pass，识别栈指针相关的操作。
• retdec-constants：好像是识别常量的类型的。看不懂。里面好像有根据debuginfo，获取data段变量类型。
• retdec-param-return：识别call指令参数的存放什么的
• retdec-simple-types：关键类型识别Pass，eqSet和equation
• retdec-write-dsm：Generate the current disassembly？
• retdec-remove-asm-instrs：Remove all special instructions used to map LLVM instructions to ASM instructions
• retdec-class-hierarchy：好像是根据RTTI和vtable搞class的继承关系
• retdec-select-fncs：如果config里面选择了部分函数，就把其他函数删了。
• retdec-unreachable-funcs：删除不可达函数？
• retdec-register-localization让所有寄存器变成局部变量
• retdec-value-protect：Protect values from LLVM optimization passes
• retdec-stack-ptr-op-remove：重要的
• retdec-remove-phi：
• retdec-write-ll：
• retdec-write-bc：
• retdec-llvmir2hll：

retdec 栈恢复算法

源码在retdec\src\bin2llvmir\optimizations\stack\stack.cpp。总体思路非常简单，分析每个load和store用到的东西，提取成一个表达式树（SymbolicTree类）。首先判断表达式树里面有没有栈指针，没有就不处理。然后尝试把整个表达式树化简，把栈指针看作0，化简成一个常量，然后把这个常量当作栈偏移，创建一个alloca去替换它。

例如，对于下面的语法树：

src/optimizers/retdec-stack/retdec-stack.cpp:142: 
-----------------------------------------------
>|   %254 = getelementptr [16777216 x i8], [16777216 x i8]* @__notdec_mem0, i64 0, i64 %253
        >| @__notdec_mem0 = global [16777216 x i8] zeroinitializer
        >| i64 0
        >|   %calcOffset249 = add i32 %0, -16
                >|   %0 = load i32, i32* @__stack_pointer, align 4
                        >| @__stack_pointer = internal global i32 5247184
                                >| i32 0
                >| i32 -16
-----------------------------------------------

被化简为：

src/optimizers/retdec-stack/retdec-stack.cpp:171: 
-----------------------------------------------
>| i32 -16
-----------------------------------------------

这个方法还是有很大问题，有许多处理不了的情况。从这个角度看，retdec确实是比ghidra差的。现在现有的开源反编译器里面也就ghidra最好了。比如如果存在memcpy这种函数的调用，由于直接传地址，所以不是load/store的形式，而是计算完地址直接传给函数了，导致没有将里面的值替换为新创建的alloca。

代码解读

• abi.cpp 主要负责提供两个函数，isStackPointer和（我们自己新增的）isMemory，判断一个值是否是栈指针。
• reaching-definition.cpp 计算load和store之间的到达定值关系？
• symbolic-tree.cpp 符号树。
  • expand操作，当初次构建符号树的时候，会从感兴趣的值开始反向遍历Use关系，生成符号树。
    • 我们适配wasm时，让栈指针的子节点为常量0。方便后续化简栈指针偏移的访问为常量（之后的化简操作会将栈指针视为常量0）。（retdec在分析非wasm程序时，会为寄存器创建对应的全局变量，初始值为0，但是我们wasm的栈指针初始值不为0，所以需要修改。）
  • simplifyNode操作，尝试将符号树化简。比如如果有算数操作，且两边都是常量，则会化简为运算后的结果。
• stack.cpp 栈分析的主体代码。遍历处理load/store指令。有三种情况：1 处理Load指令的指针，2 处理Store指令打算存进内存的值，3 处理store指令的指针
  • 对要分析的Value构建SymbolicTree（expand操作）。
  • 使用val2val这个map进行缓存，缓存已经化简过的结果，从被分析的value映射到化简后的ConstantInt。如果不在缓存里，继续后面的分析。
  • 首先判断当前的SymbolicTree里面有没有栈指针，如果没有就直接返回，放弃处理。
  • 化简当前的SymbolicTree，如果化简为ConstantInt常量，则继续处理，否则直接返回放弃处理。
  • （我们新增）使用off2alloca这个map从偏移映射到alloca指令，防止重复创建栈变量。
  • 把化简后的常量当作栈偏移，为每个不同的栈偏移创建变量。变量类型从load/store中找的好像。
  • 把当前被分析的Value替换为对应的Alloca指令。
• stack-pointer-op-remove.cpp 独立的pass，移除栈变量识别后无用的代码。

retdec 关键类型识别

源码在retdec/src/bin2llvmir/optimizations/simple_types/simple_types.cpp。感觉就是一个启发式的算法，利用库函数和DEBUG信息来恢复类型，涉及到一些指针分析的内容。比较迷惑的一点是这个Pass会运行两次，第一次应该是比较重要的，第二次涉及到一些前端的函数，主要做的好像就是针对宽字符类型参数的修复。

数据结构

• eSourcePriority：一个枚举类型，作用是定义优先级，每个ValueEntry、TypeEntry都有一个优先级，优先级越高，说明其类型信息越准确。

  • 0 | PRIORITY_NONE：默认优先级
  • 1 | PRIORITY_LIT：一般就是非用户定义的函数，如动态链接/静态链接/系统调用/IDIOM（不太明白是什么）
  • 2 | PRIORITY_DEBUG :表示该变量/函数是从debug信息中引入的。

• ValueEntry；对原生Value的封装，成员函数有value比较、hash以及getTypeForPropagation：就是获取value的类型，如果是普通指针的话就返回指向的元素类型，数组指针则返回数组内元素类型（函数名中的Propagation可能就是来自这里），如果是函数那么返回函数的返回值类型。

• TypeEntry： 同样也是对原生Type的封装，没有比较特殊的成员函数。

• EquationEntry；用于描述两个等价集的关系，就两个关系：

  • otherIsPtrToThis ： 是另一个集合的指向
  • thisIsPtrToOther ： 是另一个集合的指针

• EqSet (Equivalence set)：等价集，一个类型对应一个等价集，比较重要的成员变量有：

  public:
  	TypeEntry masterType; //主类型，会在propagate时不断更新，
  	ValueEntrySet valSet; //储存与指针有关的Value集合，propagate时会遍历
                            //这个集合，寻找优先级高的Value的类型作为主类型
  	TypeEntrySet typeSet; //储存与指针有关的Type集合，propagate时会遍历
                            //这个集合，寻找优先级高的类型作为主类型
  	EquationEntrySet equationSet; //储存有可能指向该Value的指针，实际并没有用到
  

• EqSetContainer ：储存Module中的全部等价集。

代码解读

第一次调用Pass的流程：

1. buildEqSets: 对所有全局变量，函数参数、Alloca指令调用processRoot，实际上就是为指针建立一个EqSet，并把跟它有关的Value、Type放进去。

   • processRoot(Value *v)：创建一个新的EqSet，将v加入待处理队列toProcess，并调用processValue。
   • processValue：处理待处理队列toProcess中的v，将v放入EqSet，并遍历v的所有Use，调用processUse。
   • processUse：真正的处理函数，因为use一般是各种指令，需要对不同的指令做不同的处理：
     • 通常情况就是把指令的操作数都加入待处理队列。
     • 如果是是Store指令，那指针操作数也要放入toProcess
     • 如果是常量表达式ConstantExpr，那就继续往下寻找真正Use的地方。
     • PtrToInt/BitCast：如果操作数是全局变量，那就放入val2PtrVal集合，因为ptrtoint和bitcast实际上就是把指针存在一个临时寄存器里，不知道为什么不处理alloc的指针。
     • ...

2. buildEquations：遍历val2PtrVal集合，更新equationSet，实际上就是维护指针和存指针的变量的关系。

3. propagate：在module的范围内进行的类型信息的传播与合并，优先级的作用体现在这里，优先级越高的类型会替代masterType。

4. apply：更新valSet中各个Value的类型，调用IrModifier修改类型。

5. eraseObsoleteInstructions：删除被替换掉的指令。

6. setGlobalConstants： 将没有Store指令的全局变量设置const属性，这个属性是retdec自己定义的。

第二次有不同的流程，遍历每个全局变量的Users，只处理两种指令：

• 如果是CallInst，如果全局变量为宽字符类型并且是函数的参数，则使用 IrModifier 对象将其类型更改为宽字符类型。
• 如果是ConstantExpr,那么继续往下寻找真正Use的地方，如果找到的是CallInst，就跟上面的流程基本一致。

结构分析-llvmir2hll

移植

• 首先将src/llvmir2hll目录（以及include目录）复制了过来，然后使用替换把对应路径的include替换为新路径的include。

  cp -r /sn640/retdec/src/llvmir2hll ./retdec-llvmir2hll
  cp -r /sn640/retdec/include/retdec/llvmir2hll/* ./retdec-llvmir2hll/
  cp -r /sn640/retdec/src/common ./retdec-llvmir2hll/
  cp -r /sn640/retdec/include/retdec/common ./retdec-llvmir2hll/
  cp -r /sn640/retdec/include/retdec/utils ./retdec-llvmir2hll/
  cp -r /sn640/retdec/src/utils ./retdec-llvmir2hll/
  cp -r /sn640/retdec/include/retdec/config ./retdec-llvmir2hll/retdec-config
  cp -r /sn640/retdec/src/config/* ./retdec-llvmir2hll/retdec-config
  cp -r /sn640/retdec/src/serdes ./retdec-llvmir2hll/
  cp -r /sn640/retdec/include/retdec/serdes ./retdec-llvmir2hll/
  

  在vscode里面把#include "retdec/llvmir2hll -> #include "backend/retdec-llvmir2hll 把#include "retdec/common -> #include "backend/retdec-llvmir2hll/common 把#include "retdec/utils -> #include "backend/retdec-llvmir2hll/utils

  增加cmake里面的源码 find common/ utils/ retdec-config/ serdes/ retdec-utils/ -name "*.cpp"

• 发现使用了common里面的东西，把common目录也复制过来。同理复制config目录

• 修复大量编译报错，以及新版本LLVM的变化

调用

分析src/llvmir2hll/llvmir2hll.cpp中对llvmir2hll的调用。

retypd

Intro

钻研了半年多《Polymorphic Type Inference for Machine Code》论文。看完本文后还有任何相关的问题可以问我。

跨函数的类型传播算法，可以将库函数的类型传递到代码内部。即使没有库函数识别时，也可以识别处函数内的结构体信息。

资源

retypd 是一个非常高级的反编译类型恢复算法，技术领先程度足以超出其他论文好几年。有一篇论文: 《Polymorphic Type Inference for Machine Code》

资源：

• 优先看这个介绍。
• 这个PPT比论文容易懂很多

背景

规则生成

• 复制操作：x := y，此时保守地认为，有可能是子类型赋值给了父类型变量：Y ⊑ X。
  • 由复制操作带来的数据流，类型方向是父类型。子类型赋值给了父类型。
• 指针加载：x := *p，生成：P.load.σ32@0 ⊑ X 。
• 指针赋值：*q := y，生成 Y ⊑ Q.store.σ32@0 。
• 函数调用：如果有调用y := f(x)，生成 X ⊑ F.in 和 F.out ⊑ Y 。
• icmp：两值进行比较的时候：1 bool类型是结果的子类型。2 两个被比较的值直接，随便生成一个子类型关系？

开发与使用

如何使用当前开源的代码呢？代码是一个python模块。当前开源的两个相关的使用代码有：retypd-ghidra-plugin和gtirb-ddisasm-retypd。

首先分析retypd-ghidra-plugin是如何使用retypd的。内部代码主要分为ghidra插件的java代码，和封装模块，ghidra_retypd_provider。Java代码部分通过Ghidra提供的API，从Ghidra的反编译器的IR中提取出相关的类型约束，提取为json文件。然后调用python封装模块读取并求解，结果也表示为json文件。然后Ghidra插件部分的java代码读取结果，并设置相应的类型。（注，无论是上次分析lua虚拟机，还是这次分析/bin/ls，花的时间特别久，半小时往上）

输入ghidra_retypd_provider的样例json约束文件如下。可以观察到，每个函数的约束单独分开，同时还包含一个call graph部分。

{
  "language": "x86/little/64/default",
  "constraints": {
    "FUN_00109d00": [
        "v_7456 ⊑ v_7780",
        "v_997 ⊑ int64",
        "v_1441 ⊑ FUN_00109b50.in_13",
        "v_4504 ⊑ v_1242.store.σ8@0",
        "v_6777 ⊑ FUN_00109b50.in_5",
        "bool ⊑ v_542",
        "v_2301 ⊑ null",
        "v_7379.load.σ8@0*[nobound] ⊑ v_1441",
        "v_4396 ⊑ v_1671.store.σ8@0*[nobound]",
        "v_1188.load.σ8@0 ⊑ v_1191",
        "v_1671.load.σ8@0*[nobound] ⊑ v_1720",
    ],
    "FUN_00110e10": [
        ...
    ]
  }
  "callgraph": {
    "FUN_00109d00": [
      "FUN_001158c0",
      "FUN_00115920",
      "FUN_00109b50",
      "FUN_00115b30"
    ],
    "FUN_00110e10": [
      "strcmp",
      "strlen",
      "FUN_001158c0",
      "getgrnam",
      "strcpy"
    ],
    ...
  }
}

输出ghidra_retypd_provider的样例json结果文件如下。可以观察到，包含两种类型的结果，分别是结构体和函数。结构体包含内部的成员及类型。函数块描述了函数的各个参数的类型。在这里的自定义encoder中定义了转json的函数。

这一点其实很奇怪，似乎该插件关注的核心是函数参数类型。这里后续解析和类型设置也说明了这一点。

[
  {
    "type": "struct",
    "name": "struct_545",
    "fields": [
      {
        "name": "field_0",
        "type": "char1_t*",
        "offset": 0
      },
      {
        "name": "field_1",
        "type": "char1_t[4]",
        "offset": 168
      }
    ]
  },
  {
    "type": "function",
    "name": "function_260",
    "params": [
      {
        "index": 0,
        "type": "char1_t[4]"
      }
    ],
    "ret": "char1_t[0]"
  },
  ...
]

接着我们看ghidra_retypd_provider内部是如何调用retypd的。

• 使用SchemaParser.parse_constraint解析每个约束项（SubtypeConstraint），它保存子类型关系左右两边的变量（DerivedTypeVariable）。每个函数的约束项放到一个集合里，再按函数名字放到map里，然后构建Program：

  program = Program(
      CLattice(),
      {},
      parsed_constraints,
      callgraph,
  )
  

  这里parsed_constraints就是准备好的那个map。callgraph都不用动，就是Dict[str, List[str]]。前两个参数分别是types: Lattice[DerivedTypeVariable]和global_vars: Iterable[MaybeVar]。

• 使用Solver去求解约束：

  config = SolverConfig(top_down_propagation=True)
  solver = Solver(program, config, verbose=LogLevel.DEBUG)
  _, sketches = solver()
  

  查看solver的__call__方法，可以发现返回类型是Dict[DerivedTypeVariable, ConstraintSet]和Dict[DerivedTypeVariable, Sketch]。

• 传入CTypeGenerator，得到最终的类型结果。

  gen = CTypeGenerator(
      sketches,
      CLattice(),
      CLatticeCTypes(),
      int_size,
      pointer_size,
  )
  return list(gen().values())
  

  CTypeGenerator的__call__方法的返回类型是Dict[DerivedTypeVariable, CType]。

根据这里，每个规则大致就是var1 ⊑ var2或者var1 <= var2，然后两边的变量就是DerivedTypeVariable类型的。因此，上面结果里返回的map其实就能够用来查每个变量的类型。

S-Pointer and S-Field⊕/⊖ 通过搜索代码，可以得知，至少在retypd-ghidra-plugin和gtirb-ddisasm-retypd中是没有和这个相关的规则的生成的。

retypd ghidra 插件

在我的fork仓库里可以直接下载到构建好的插件，修改版Ghidra，以及docker镜像。同时提供了给retypd的样例输入和输出。

通过修改 GhidraRetypd.zip中的extension.properties，可以绕过ghidra插件安装时的版本检查

version=10.2.3

安装Ghidra插件：

1. 打开 Ghidra 软件，点击 "File" 菜单，选择 "Install Extensions" 选项。
2. 在弹出的 "Install Extensions" 窗口中，点击 "Browse" 按钮选择你要安装的扩展程序。
3. 选中你要安装的扩展程序文件（通常是一个 zip 压缩文件），然后点击 "Open" 按钮。
4. 点击 "OK" 按钮开始安装扩展程序。在安装过程中，Ghidra 软件会自动解压缩扩展程序文件，并将它们安装到正确的目录中。
5. 安装完成后，重启 Ghidra。

算法详解

• 首先阅读这个PPT和这个论文《Saturation algorithms for model-checking pushdown systems》，学会B¨uchi发现， Caucal提出的这个saturation算法。
• 然后阅读论文，学习其中基于saturation算法改进的部分。

自动机基础 Saturation algorithms

资料：

• 《Pushdown systems》了解下推自动机
• 《Saturation algorithms for model-checking pushdown systems》了解Saturation algorithms相关的背景概念。

有两个重要结论：

• 下推系统可达的栈内容形成了一个正则语言，因此可以表示为有限状态自动机。但是最初提出的算法是指数级的。后面有人提出了多项式级的算法，核心思想就是引入一个saturation process，转换被逐渐地加入有限自动机。（这个结论没有被retypd使用）
• 下推系统定义了配置（状态加栈字符串）之间的转换关系，可以多项式时间内构建一个带输出的有限状态自动机（transducer）识别这些转换关系。（retypd使用的结论）

有限自动机

• $\Sigma$ 是自动机的字符集。$\Sigma^{*}$ 是字符串的集合。 $\Gamma^{\leq n}$ 是长度最多为n的字符串集合。
• 一个在字符集 $\Sigma$ 上的自动机 $\mathcal{A}$ 是一个元组： $(\mathbb{S},\mathcal{I},\mathcal{F},\delta)$ 分别代表有限的状态集合，初始状态集合，最终状态集合，转换规则集合 $\delta \subseteq \mathbb{S} \times \Sigma \times \mathbb{S}$ 表示从一个状态遇到一个字符，转换到另外一个状态。
  • 有时会把字符集写进来 $(\mathbb{S},\Sigma,\mathcal{I},\mathcal{F},\delta)$ 变成五元组
• $s \overset{a}{\underset{\mathcal{A}}{\longrightarrow}} t$ 表示自动机 $\mathcal{A}$ 有这样一个转换 $(s,a,t)$
• $s \overset{w}{\underset{\mathcal{A}}{\Longrightarrow}} t$ 表示自动机读入字符串w之后可以转换到t。

下推系统 pushdown system 与 P-自动机

和下推自动机的区别：pushdown system是自动机的简化版本。当我们用PDS建模程序的时候，有时不太关注读入和识别字符，而是关注栈状态的转移。

和自动机的区别在于没有识别字符串这种概念。自动机一般只能用来识别字符串，有初始态，终止态，遇到某个字符的时候触发转换规则。这里的下推系统则不是识别字符串的，即转换规则里不需要读入字符，直接改变状态和栈内容。这里下推系统直接主要关注栈上的内容字符串。

一个下推系统是四元组 $(Q,\Gamma,\bot,\Delta)$

• $Q$ 是有限的控制状态的集合
• $\Gamma$ 是有限的栈字符集
• $\bot \in \Gamma$ 是一个特殊的底部栈字符
• $\Delta \subseteq (Q \times \Gamma) \times (Q \times \Gamma^{\leq 2})$ 是转换的集合。表示在一个状态从栈上弹出一个字符，转换到另外一个状态并压入一个字符串。
• Configuration表示系统状态，是 当前状态 $\in Q$ 和 当前栈字符串 $\in \Gamma^{*}$ 的二元组。
• 不考虑弹出超过栈底的情况。所以有时会引入特殊底部栈字符，然后要求规则不会把这个符号弹出来。

Pushdown system （PDS）可以用来分析程序

• 程序表示
  • 状态Q保存程序的全局变量
  • 栈反映程序执行的调用栈
  • 栈上字符编码程序局部变量：比如编码为 当前program counter 和 局部变量的二元组。
• 一些例子
  • 状态 $pAw$, 这里 $p$ 表示状态，代表全局变量， $Aw$ 表示栈。其中 $A$ 表示当前的PC和局部变量，w表示调用栈中，被“暂停”执行的程序状态，包括返回地址和局部变量情况。
  • 状态转换 $pA \rightarrow qB$ 表示执行一个普通语句。
    • 全局变量可能发生修改，从 $p$ 变成 $q$ ，
    • 栈深度不变，但是从A变成B，表示当前PC和局部变量发生了变化。
  • 状态转换 $pA \rightarrow qBC$ 表示函数调用
    • 栈深度增加了，B里面包含了返回地址以及调用者的局部变量状态。现在压入了被调用者的栈。
  • $pA \rightarrow q\epsilon$ 表示函数返回
    • 栈上弹出了一个字符，表示弹出了一个调用栈。

PDS的可达性问题

给定一个PDS和两个configuration $c,c'$，是否能从 $c$ 走到 $c'$ 状态？

$$ { w \in \Gamma^{*} \mid \exists q \in Q, (q_{0},\bot) \Rightarrow (q,w) } $$

即求出这样一个集合，从起始状态 $(q_{0},\bot)$ 出发能推导到的所有状态 $(q,w)$ (这里状态 $q \in Q$ 任意)，其中字符串w组成的集合。

一个非常重要的结论是，这里可达的字符串集合形成了正则语言。 这意味着函数调用时的状态转换可以用一个有限状态自动机表示。

PDS的configuration的正则性：

• 背景：众所周知，能被确定有限状态自动机识别的语言是正则（regular）语言。而说到语言，我们会想到根据语法生成的规则，最后推导出很多可以被接受的字符串，但是语言本质也就是一种无限的字符串的集合。
  • 如果是有限的话，直接对每个字符串用or连接就完全匹配了。所以一般讨论的都是无限的字符串集合。
• 定义1：如果某个配置集合 $C$ 是正则的，那么对任意的状态 $p \in Q$ （即不管状态），在这个配置集合里面的所有字符串w构成的集合， ${ w \in \Gamma^{*} \mid (p,w) \in C}$ 是正则的。即栈状态构成正则语言。
  • 简单来说，不管state，如果栈上字符的集合构成正则的语言，则这个configuration集合是正则的。
• 定理1，初始状态可达的配置集合的正则性：
  • 定义：初始配置：任意状态，但是栈为空（仅有 $\bot$ 符号）的配置
  • 任意pushdown system，从初始配置出发，可达的配置是正则的。
• 定理2：后推闭包的正则性：给定一个正则配置集合C，基于自动机规则任意后推形成的闭包集合也是正则的。
  • 写作：$Post^*_{P}(C) = { c' \mid \exists c \in C, c \underset{P}{\Longrightarrow} c' }$ 从任意的C中配置开始，在自动机P下能推导出c'，则c'属于集合。
  • 这一定理能从定理1推出：构建一个新自动机P'，增加很多新的state，使得当前配置集合都是初始配置。这里定理里的后推可得到的配置集合其实就是可达的配置集合。
• 倒推闭包的正则性：正则集合的倒推集合，即另外一个配置集合Pre*(C)，能够推理得到当前集合C。当前集合是正则的，则Pre*(C)也是正则的。
  • 原因：有时候想要基于程序的错误状态，倒退前面的可达状态。
  • 证明：思想是，构建新的自动机P'，规则和P是反着来的。
    • 如果P有个规则是 $qA \rightarrow p$ 即弹出了字符A。我们P'增加反着来，压入字符A的规则 $pX \rightarrow qAX$。即对于任意字符X，都允许压入AX。
    • 如果P有个规则是 $qA \rightarrow pBC$ 弹出A压入BC。则我们需要增加两个规则。
      • $pB \rightarrow r_{(C,q,A)}$
      • $r_{(C,q,A)} C \rightarrow q A$
      • 直接插入规则的问题在于，下推自动机左边一般只能匹配一个栈顶字符，右边则可以为空，也可以压入两个字符。这里我们需要考虑同时按顺序存在BC字符的情况。
      • 借助中间状态 $r_{(C,q,A)}$ 我们
    • 一致性：如果在P中有两个状态可以互推，当且仅当我们P'中这两个状态可以反着互推。而且P'满足上面定理的要求，然后应用上面正推的定理，成功证明反推定理。

和retypd的PDS对应：我们构建的PDS表达的是子类型之间的转换关系。但是实际构建出来可能存在很多初始状态不可达的序列。例如如果有规则 $A.load \sqsubseteq B$ 我们增加初始状态的转换，使得初始状态可达 (A/B, $\bot$) 的配置。但是规则并不允许 $(A, \bot) \rightarrow (A, .load)$ ，否则存在子类型关系 $A \sqsubseteq A.load$。也因此，这里构建的自动机没有用在retypd中。

PDS对应的自动机

有一个PDS $\mathcal{P}=(P, \Gamma, \Delta)$，我们对应有一个有限自动机 $\mathcal{A}=(Q, \Gamma, P, T, F)$

• PDS的栈字符集 $\Gamma$ 被用作有限自动机的字符集。PDS栈字符原本用来表示局部变量和PC。
• PDS的控制状态（表示全局变量），被用作有限自动机的初始状态。
• 我们称，有限自动机接受配置 $pw$ ，如果自动机从状态p开始，接受字符串w之后能停止在终结态。而且对应每个PDS都能构造出这样的自动机。
  • 直观上理解：对任意的state（代表了程序的全局变量状态），此时可能的栈情况是什么样的？这些所有可能的栈情况可以用一个有限自动机来表达。
  • 上面提到，不考虑状态，单把栈上字符串拿出来，形成的也是正则语言。这里其实表达的是一个意思。每个configuration的状态作为初始状态，然后存在一个P-有限自动机匹配栈上的内容，其实就是说明了栈上形成的是正则语言。

Pre(S)的Saturation Algorithm

• 相关符号总结
  • $\Delta$: pushdown system的下推规则
  • $\delta$: P-自动机的状态推理规则。后面会不断增加规则，构成一个递增的规则序列。
  • $Q$: pushdown system的状态集合，也是P-自动机的初始状态
  • $\mathcal{F}$: P-自动机的终止状态集合
  • $\mathcal{A}$: P-自动机。包括状态集合 $\mathbb{S}$, 初始状态 $Q$, 推理规则 $\delta$ 和终止状态 $\mathcal{F}$。
  • $\mathcal{L}(\mathcal{A})$: 表示A接受的语言。
  • $\mathcal{B}$: 需要构建的新自动机，接受 $Pre^{*}_P (\mathcal{L}(\mathcal{A}))$
• Saturation Algorithm算法

  • 前提：已知一个下推系统 $P=(Q,\Gamma,\bot,\Delta)$ ,和对应的P-自动机 $\mathcal{A}=(\mathbb{S},Q,\delta,\mathcal{F})$

  • 目标：构建出一个新的自动机 $\mathcal{B}$ 接受语言 $Pre^{*}_P (\mathcal{L}(\mathcal{A}))$

  • 过程：构建一个自动机的序列 $(\mathcal{A}{i}){i \in [0,N]}$

    • 其中其他部分都是相同的，状态数量是相同的，只有转换规则 $\delta_i$ 不同。
    • 保证转换规则只会增加新的规则： $i \in [0,N-1]$, $\delta_{i} \subseteq \delta_{i+1}$
    • 最后转换规则会收敛，达到不动点： $\delta_{i+1}=\delta_{i}$
    • 每次至少增加一个规则，因此程序最多走 $|Q|^{2} |\Gamma|$ 步
      • 作为一个有限状态自动机，这里只对Q状态增加边，每两个状态之间最多 $|\Gamma|$ 个规则。

  • 算法：如果有一个规则 $pA \rightarrow qw$ ，同时现在的P-自动机存在一个路径 $q \overset{w}{\underset{\mathcal{A}_{i}}{\Longrightarrow}} s$ 我们给P-自动机增加一个新的转换规则 $p \xrightarrow[]{A} s$

    

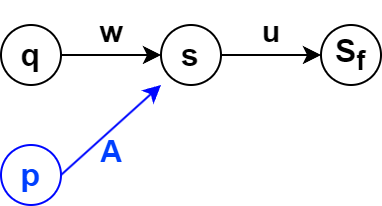
    p Au -> q wu。原有自动机为黑色部分，u代表未知任意字符串，即代表的是路径，内部省略了具体的其他节点。意味着从状态为q栈为空的状态，能够接受一个字符串wu。

    然后我们新增了这样一条规则，使得状态为p，字符串为Au也被接受了。

    规则的构建使得，某个下推系统的前驱规则的节点被覆盖到了。而最后目的自动机 $\mathcal{B}$ 由于达到了不动点，因此关于下推系统P的前驱规则封闭。

  • 证明过程的不变量：在这个自动机转换规则的序列中，存在一些始终为真的条件。如果自动机存在转换规则 $p \xrightarrow[]{A} s$ ，那么以下两个性质始终满足满足。

    • 如果状态s属于下推系统P的状态：在下推系统P中存在规则 $pA \overset{}{\underset{P}{\Longrightarrow}} s$。这是一个弹出栈字符的规则。
    • 如果状态s属于其他状态，即不属于下推系统P的状态：对于任何从状态s出发能被接受的字符串u，配置 $(p,Au)$ 属于 $Pre^{*}_P (\mathcal{L}(\mathcal{A}))$
    • 从这个不变关系，可以推出， $\mathcal{L}(\mathcal{A}_i) \subseteq Pre^{}_P (\mathcal{L}(\mathcal{A}))$ ，即每个A的语言都是我们目标的子集。 特别地， $\mathcal{L}(\mathcal{B}) \subseteq Pre^{}_P (\mathcal{L}(\mathcal{A}))$ 最终迭代的不动点也是这样。

  • 最小关系：我们如果只关注状态在Q中（下推系统的状态）的部分，那么关系只在 $(Q \times {\varepsilon}) \times (Q \times \Gamma)$ 上被添加 1. 左边都是初始状态; 2. 转换规则都是接受了一个字符。 这里增加的关系可以被看作是一个最小关系 $\mathcal{R}$

    • $pA ; \mathcal{R} ; q$ 如果存在规则 $pA \rightarrow q$
    • $pA ; \mathcal{R} ; q$ 如果 $rB ; \mathcal{R} ; q$ 并且 $pA \rightarrow rB$ 在规则中。
      • 这里关系 $\mathcal{R}$ 似乎会对每个带栈字符的状态创建一个无字符的对应状态？比如这里为 $rB$ 引入中间状态
    • $pA ; \mathcal{R} ; q$ 如果存在规则 $pA \rightarrow rBC$，并且存在状态 $s\in Q$，关系 $rB ; \mathcal{R} ; s$ 和 $sC ; \mathcal{R} ; q$
      • 这里 $q$ 仿佛直接代表了 $rBC$

描述派生（可达）关系的 Transducer

基础概念：

• Finite State Transducer 其实就是带有输出的有限状态自动机（finite state automaton）。

• 派生关系 $Deriv_{P}$：描述任意两个字符串之间的关系： $Deriv_{P} ={ (u,v) \in \Gamma^{*} \mid (q_{0},u) \overset{}{\underset{P}{\Longrightarrow}} (q_{f},v) }.$

  • $Deriv_{P} \subseteq \Gamma^{} \times \Gamma^{}$ 。是字符串之间的关系。

• 操作：$A_{+}$ 表示压入单个符号的操作 push A（$A \in \Gamma$ 是字符）。 $A_{-}$ 同理。

  • 操作集合 $\Gamma_{+}={ A_{+} \mid A \in \Gamma}$ push操作的集合， $\Gamma_{-}$ 同理。 $\overline{\Gamma}=\Gamma_{+} \cup \Gamma_{-}$ 表示两个的并集。
  • 操作序列： $\alpha=\alpha_{1} \ldots \alpha_{n} \in \overline{\Gamma}^{*}$ 表示一系列操作。
    • 例如， $pA \rightarrow qBC$ 的操作序列是 $A_{-}C_{+}B_{+}$
  • 操作转换关系： $u \overset{\alpha}{\underset{}{\leadsto}} v$ 表示栈状态 $u \in \Gamma^{*}$ 在操作 $\alpha$ 下变成了栈状态 $v$。
  • non-productive序列：无法被应用的栈序列，常常是这种 $B_{+} C_{-}$ 先push再pop一个不同符号的序列，刚压入B，怎么可能栈顶弹出C呢？
    • 就像下面对比图先走橙色边再走蓝色边一样。

• 对比自动机和transducer

  

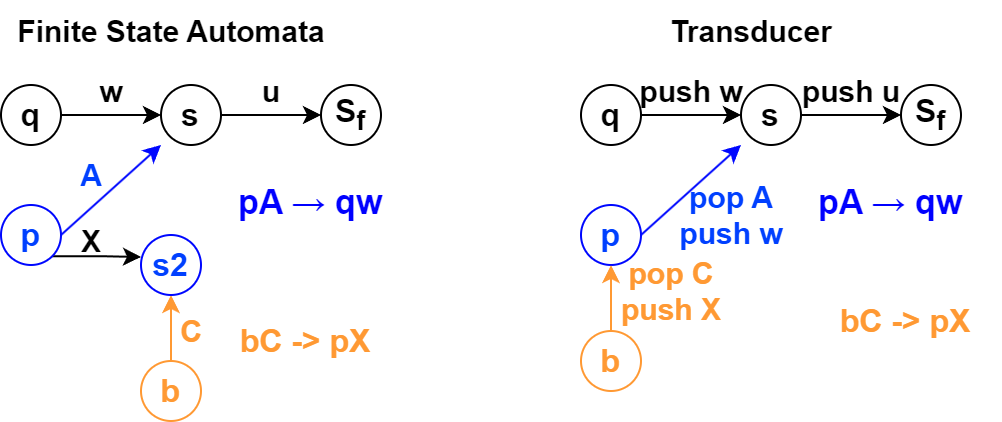
  这里可以看到，transducer的状态和PDS是完全对应的，前面的自动机则仅是初始状态和PDS相同，只有栈为空的时候才对应PDS对应的状态。

  Transducer 每条边上也只能push或pop一个字符，这里是简略写法，隐藏了中间的状态。但是是否打破了Transducer和PDS状态的对应关系？并没有，如果要求PDS每次也只能增加或者减少一个栈字符，则两边还是对应的。

• 行为集合 $Behaviour_{P}$ 表示下推系统P，不管是否non-productive，可能走出的所有栈操作序列的集合。

  • 即我现在只需要管状态转换，不需要管栈操作的应用。
  • 即画出上面的转换图，然后随便沿着边走

• $Behaviour_{P}$ 和 $Deriv_{P}$ 的关系：对于任何在行为集合的操作序列， $\alpha \in Behaviour_{P}$ ， 两个字符串属于派生关系集合 $(u,v) \in Deriv_{P}$ 当且仅当 这两个字符串存在操作关系 $u \overset{\alpha}{\underset{}{\leadsto}} v$ 。

  • 然而这个定义不太行，因为 (1) $Behaviour_{P}$ 有很多不合法的序列。(2) 存在刚push就pop的冗余序列，如 $A_{-} B_{+} A_{+} A_{-} C_{+} C_{-}=A_{-} B_{+}$ 。

• 简化关系 $\mapsto$ ：表示一个栈操作序列被简化为另外一个栈操作序列。消除了上面的这种刚push就pop的冗余行为

  • 例如 $B_{-}A_{+}A_{-}C_{+} \mapsto B_{-}C_{+}$

• 操作序列集合在简化操作下维持正则性：如果一个操作序列集合R内的每个操作都被 $\mapsto$ 简化，那么新的集合 $Red(R) = { Red(\alpha) \mid \alpha \in R }$ 也是正则的

• 操作序列自动机的简化算法： $Red(R)$ 能在 $\mathcal{O}(|\mathcal{A}|^{3})$ 的复杂度构建出来。

• 简化并移除non-productive序列的操作集合 $RP_{P}$

  • 移除non-productive序列：简化后很容易识别，直接扫描找先push再pop的序列。因为如果push的字符和pop的字符不同则不合法，相同则说明化简没有结束。
  • 性质：可以推出里面的序列必然只会先pop再push。

• 最终的结论：

  • $Deriv_{P}$ 的关系 $(w_{1},w_{2})$ 对应到transducer 必然是，找出两个串的公共后缀，然后先pop w1的前缀，然后push w2的前缀。
  • $Deriv_{P}$ 对应的 Transducer 可以在多项式时间内被构建出来。

核心在于，将状态转换改为了一个push pop栈的序列。即，如果有一个 $pA \rightarrow rw$ 规则，那么我们这里构建一个序列：pop A，push ...(构成w的几个字符)。表示栈上的变化关系。

然后使用饱和（Saturation）算法。这里需要每条边上的操作只能压入或者弹出单个字符。即找到两个路径上能化简的状态，然后直接连过去，标上化简后的操作序列。

这里的饱和（Saturation）算法才是后面retypd使用的。

retypd 基础符号

使用的符号

• $\mathcal{V}$: 类型变量的集合
  • 在这个集合里包含一系列类型常量，作为一种符号描述。这些类型常量可能形成一个lattice，但是我们不解释它们。
• $\Sigma$: 字段标签 field label。不一定是有限的。主要的符号如下：
  • $\mathsf{.in}_L$ 函数在位置L的输入
  • $\mathsf{.out}_L$ 函数在L位置的输出
  • $\mathsf{.load}$ 可读的指针
  • $\mathsf{.store}$ 可写的指针
  • $.\sigma\mathsf{N@k}$ 在偏移k处有一个N bit的成员。
• 函数 $\langle \cdot \rangle : \Sigma \to { \oplus, \ominus }$: 从结构体label映射到 ${ \oplus, \ominus }$ 表示variance，协变和逆变属性
• 派生的类型变量 derived type variable (定义3.1)：形为 $\alpha w$ ，其中类型变量 $\alpha \in \mathcal{V}$ and 字段标签 $w \in \Sigma^*$.
• 标签 $\ell$ 的variance (定义3.2)，指的是前面的类型变量的类型如果发生变化时，带标签的派生类型变量的variance的变化方向。 $\alpha.\ell$ 和 $\beta.\ell$ 中，如果 $\alpha$ 是 $\beta$ 的子类型。
• 约束 $c$ (定义3.3)有两种形式。约束的集合用 $\mathcal{C}$ 表示
  • 存在形式: (派生)类型变量X存在
  • 子类型形式：(派生)类型变量X是Y的子类型。
  • 约束的推导 $\mathcal{C} \vdash c$ 表示约束能从原约束集合中，由那些规则派生出来。
  • 约束中的自由变量定义 $\exists \tau . \mathcal{C}$ 表示，存在变量 $\tau$ 满足了约束集合。
• Type Scheme类型方案，表示一个泛型的函数。 $\forall{\overline{\alpha}}.{\mathcal{C}}\Rightarrow{\beta}$ 表示在约束C的条件下，带有模板变量集合 $\overline{\alpha}$ 的泛型类型 $\beta$
  • 仅增加约束： $\forall \tau . C \Rightarrow \tau$ 表示仅对类型 $\tau$ 增加约束。
    • 例如 $\forall \tau . (\tau.\mathsf{in}.\mathsf{load}.\sigma\mathsf{32@4} \sqsubseteq \tau.\mathsf{out}) \Rightarrow \tau$ 表示函数返回了参数在4字节offset位置的成员。
  • 和约束的关系：基本是对应的。可以想象为我们主要关注约束，任何类型方案都可以理解为，声明一些通配符变量，然后定义一些约束。例如 $\forall \alpha . (\exists \tau . \mathcal{C}) \Rightarrow \alpha$ 。通过引入新的类型变量，可以让最右侧总是等于单个变量。如果能把约束里每个类型变量解出来，那么这个泛型也很容易得到。
  • 和sketch的关系。通过inferShapes算法将约束求解为变量映射到sketch的树/自动机结构。

常见术语

• pushdown system: 在基本的自动机的基础上，额外增加了一个栈结构。
• non-structural subtyping: 即子类型关系不一定非要结构完全相同（在structural subtyping中只能叶子节点不同）。尤其是在有结构体和对象这种情况。见"Type Inference with Non-structural Subtyping"

规约规则

• T-Left/T-Right/T-Prefix: 如果存在约束 $\alpha \sqsubseteq \beta$ ，则 $\alpha$ 和 $\beta$ 存在。如果存在一个带field label的派生变量，则原始变量存在。
  • 这意味着在算法中我们在访问约束时会创建对应变量节点。
• T-InheritL / T-InheritR: 子类型能安全代换父类型。父类型如果能带一个field label，则子类型带有相同的field label的派生变量也存在。
• S-Refl: 反射性，自己是自己的子类型。
• S-Field$_\oplus$ / S-Field$_\ominus$: 如果field label的variance是协变 $\oplus$，则原变量子类型关系在带上标签后保持。否则反过来。
• S-Pointer: 指针存入的类型是取出的子类型。

sketches 约束的求解结果被表示为sketches。每个value关联上一个sketch，包含该value的所有能力，即能否被store，能否访问指定的偏移。同时sketch还包含一个可自定义的lattice，用来传播类似于typedef这种类型。

我们分析的不是具体的程序中的变量，而是他们的类型和类型之间的关系。因为复杂的约束关系，我们会把类型再设为一个类型变量，称为DataTypeVariable，DTV。

什么是Sketches：一个派生类型变量DTV，可能有各种各样的能力，比如可以在offset为4的地方load出一个四字节的值 （.load.σ32@4）。首先可以遍历所有的约束关系，比如v_4504 ⊑ v_1242.store.σ8@0，对每个关系单独看两边的变量，然后看比如v_1242是否被直接这样取过offset，然后把这些操作收集起来。但是这样还不够，因为可能因为约束的存在，其他变量能做的操作，它因为约束，应该也能做。这些都求解出来，得到的数据结构就是一个Sketch。

一个Sketch才是真正直接代表一个具体的类型。是一个树状的类型结构。这个树的边上标记了field label，节点上标记了类型lattice上的元素。

基于程序操作的约束生成

• 变量复制/赋值：要么两边类型相同，要么根据安全代换原则，子类型被赋值为父类型。
• 指针读取：增加field label。
  • 指针的读和写能力分开考虑。子类型方面特殊处理。
• 函数调用：参数父类型，返回值子类型。
  • 单独的类型变量规则是structural的，即子类型和父类型的能力必须一致。但是在函数调用时，可以遗忘一些能力。

规约算法：概述（Section 5）

约束的简化

类型，以及函数的类型到底应该怎么表示？

• 格表示的类型：对于单个固定大小的基本类型，可以使用lattice结构以及一个偏序关系表示类型。子类型为格上的偏序关系
• 对于复杂的具有能力的类型，比如访问某个偏移字段的能力，加载出值的能力，则类似结构体的子类型关系，子类型允许具有更多能力，安全代换父类型。
• 函数的类型则涉及到泛型的类型方案的表示 $\forall{\overline{\alpha}}.,{C}!\Rightarrow!{\tau}$ 。为函数的输入和输出类型创建类型变量，然后得到一个变量的最小约束集合表示这个函数的类型。
  • 例如通用的恒等函数，直接将参数返回，表示为，对任意的类型X，返回值的类型也是X。对应我们的表示可能是 $F.in \sqsubseteq F.out$
• PDS = （未化简，或者简化后的）约束 = 类型方案 type scheme

我们为什么要简化约束？ 为了减少无用的自由变量，降低约束集的增长率。令 $\mathcal{C}$ 表示由抽象解释生成的过程的约束集，并且 $\overline{\alpha}$ 是 $\mathcal{C}$ 中的自由类型变量集。我们其实已经可以使用 $\forall{\overline{\alpha}}.,{\mathcal{C}}!\Rightarrow!{\tau}$ 作为过程类型方案中的约束集，因为合法调用 $f$ 时使用的输入和输出类型显然是满足 $\mathcal{C}$ 的。

然而，实际上我们不能直接使用这个约束集，因为这会导致在嵌套过程中产生很多无用的自由变量，并且约束集的增长率很高。如果一个函数没有调用其他函数，则确实约束集就自己。但是当函数调用别人，其他函数又调用更其他的函数，此时每次为一个函数推理类型时，就会牵涉进来所有这些涉及的函数的约束。因此化简约束是非常有必要的（TODO，是否可以根据约束的性质，判断它是否需要牵涉进来？）。

这个简化算法的输入是，从一个函数的推断得到的一个类型方案 $\forall{\overline{\alpha}}.,{C}!\Rightarrow!{\tau}$ （包括自由类型变量，约束，和泛型），并创建一个较小的约束集 $\mathcal{C}'$，使得任何由 $\mathcal{C}$ 对 $\tau$ 的约束也被 $\mathcal{C}'$ 所蕴含。

相反，我们寻求生成一个简化的约束集 $\mathcal{C}'$，使得如果 $c$ 是一个“有趣”的约束，并且 $\mathcal{C} ;\vdash; c$，那么 $\mathcal{C}' ;\vdash; c$ 也同样成立。但什么让一个约束变得有趣呢？

• 能力约束，表示某个dtv有某个field label
• 递归类型约束： $\tau.u {;\sqsubseteq;} \tau.v$
• 涉及常量类型的约束： $\tau.u {;\sqsubseteq;} \overline{\kappa}$ 或者 $\overline{\kappa} {;\sqsubseteq;} \tau.u$ 其中 $\overline{\kappa}$ 是类型常量.

Roadmap

1. （A.）收集文字格式的初始约束，构建初始图。插入外部函数已知的参数类型。
2. （F.1）约束简化算法。简化后的约束就是type schemes。这里对每个强连通分量后序遍历进行处理，处理完的分量内的type schemes保存下来，等待实例化。
   1. 基于约束集合构建初始图。子类型关系增加标记为1的边。对标签增加和减少的关系，增加对应push/pop的边。
      1. 比如对于dtv F.in_a.load.off_4_size_8 构建一系列图节点 F -> F.in_a -> ... -> F.in_a.load.off_4_size_8。
      2. 对于约束关系两边的dtv，连接边（边上标记1）。
   2. 运行Saturation算法，将 push α -> 1 -> pop α 这种边序列增加shortcut边。应用S-Pointer的实例化规则

• Step 3: Identify the “externally-visible” type variables and constants; call that set E.
• Step 4: Use Tarjan’s path-expression algorithm to describe all paths that start and end in E but only travel through E c.
• Step 5: Intersect the path expressions with the language (recall _)*(forget _)*.
• Step 6: Interpret the resulting language as a regular set of subtype constraints. (“forgets” on the right, “recalls” on the left)

3. （F.2）构建sketches（为每个类型变量，比如函数类型）（自底向上遍历call graph的顺序），同时细化具体类型。
4. （4.3）最后转换sketches到C类型。

类型恢复本质上是三层分析的叠加：

• 指针和数字类型的区分。
• 指针能力分析。
• 自定义的typedef常量类型传播。

本质上，retypd在前两者里用的是快速的steensgaard的指针分析，在最后这层的分析上用的是Anderson的指针分析算法。

retypd为什么不直接采用steensgaard的类型恢复？因为常量用不了，merge了直接变成父类型，基本无法传播自定义的typedef类型。。

对于每个SCC看作按需分析。每个SCC能够简化算法计算出对应的summary。

无约束的下推系统 Unconstrained Pushdown Systems

无约束的含义：TODO。可能是表示没有限制栈符号和转换规则的有限性？

核心思路： 下推系统 $\mathcal{P}_\mathcal{C}$ 的转换序列，可以直接对应上基于约束集合 $\mathcal{C}$ 上的子类型推导判断的推导树。

定义：一个无约束下推系统是由三个部分组成的元组 $\mathcal{P} = (\mathcal{V}, \Sigma, \Delta)$，其中 $\mathcal{V}$ 是控制位置的集合，$\Sigma$ 是栈符号的集合，而 $\Delta$ 是包含在 $(\mathcal{V} \times \Sigma^)^2$ 内的（可能无限）转换规则的集合。转换规则表示为 $\langle X; u \rangle \hookrightarrow \langle Y;v\rangle$，其中 $X,Y \in \mathcal{V}$ 且 $u,v \in \Sigma^$。我们定义配置的集合为 $\mathcal{V} \times \Sigma^*$。在配置 $(p,w)$ 中，$p$ 称为控制状态，$w$ 称为栈状态。

注意到，我们既不要求栈符号的集合也不要求转换规则的集合是有限的。这种自由度是为了模拟推导规则 S-Pointer， 正如图3的推导规则 S-Pointer 所示，它对应于一个无限的转换规则集。

为什么要用下推系统？ 下推系统能很好地反映类型关系关于能力的传递关系，反映在下推系统上就是后缀子串的关系。

• 转换关系定义：一个无约束的下推系统 $\mathcal{P}$ 确定了一个转换关系 $\longrightarrow$ 在配置集合上： $(X,w) \longrightarrow (Y,w')$ 如果存在一个后缀 $s$ 和一个规则 $\langle {X}; {u} \rangle \hookrightarrow \langle {Y}; {v} \rangle$，使得 $w = us$ 和 $w' = vs$。$\longrightarrow$ 的传递闭包表示为 $\stackrel{*}{\longrightarrow}$。
  • 这里的公共后缀s，就可以想象为类型的能力。比如各种偏移里的字段。然后前缀类型变量，比如两个结构体类型，如果符合子类型关系，则对应的访问相同的字段得到的类型变量，则也存在子类型关系。

有了这个定义，我们可以陈述我们简化算法背后的主要定理。这里一个类型对应一个 $(\mathcal{V} \cup \Sigma)^*$ 字符串。

设 $\mathcal{C}$ 是一个约束集合，$\mathcal{V}$ 是一组基类型变量集合。定义 在类型变量和标签集合构成的两个字符串之间的关系 $(\mathcal{V} \cup \Sigma)^* \times (\mathcal{V} \cup \Sigma)^*$ 的一个子集 $S_\mathcal{C}$， 通过 $(Xu, Yv) \in S_\mathcal{C}$ 当且仅当 $\mathcal{C} ;\vdash; X.u {;\sqsubseteq;} Y.v$。 那么 $S_\mathcal{C}$ 是一个正则集合，并且可以在 $O(|\mathcal{C}|^3)$ 时间内构造一个识别 $S_\mathcal{C}$ 的自动机 $Q$。

证明：基本思想是将每个 $X.u {;\sqsubseteq;} Y.v \in \mathcal{C}$ 作为下推系统 $\mathcal{P}$ 中的一个转换规则 $\langle {X}; {u} \rangle \hookrightarrow \langle {Y}; {v} \rangle$。 此外，我们为每个 $X \in \mathcal{V}$ 添加控制状态 ${^#{Start}}, {^#{End}}$ 及其转换 $\langle {{^#{Start}}}; {X} \rangle \hookrightarrow \langle {X}; {\varepsilon} \rangle$ 和 $\langle {X}; {\varepsilon} \rangle \hookrightarrow \langle {{^#{End}}}; {X} \rangle$。 目前， 假设所有标签都是协变的，并且忽略规则 S-Pointer。 通过构造，$({^#{Start}}, Xu) \stackrel{}{\longrightarrow} ({^#{End}}, Yv)$ 在 $\mathcal{P}$ 中当且仅当 $\mathcal{C} ;\vdash; X.u {;\sqsubseteq;} Y.v$。 Büchi [27] 保证，对于任何标准（非无约束）下推系统中的两个控制状态 $A$ 和 $B$， 所有满足 $(A, u) \stackrel{}{\longrightarrow} (B, v)$ 的 $(u,v)$ 对组成的集合是一个正则语言； Caucal [8] 给出了一个构造识别这种语言的自动机的饱和算法。

在完整的证明中，我们增加了两个创新之处：首先，我们通过将variance数据编码到控制状态和转换规则中，支持逆变堆栈符号。 第二个创新之处涉及到 S-Pointer 规则；这个规则是有问题的，因为自然的编码将导致无限多的转换规则。 我们将 Caucal 的构造扩展为在饱和过程中懒惰实例化所有必要的 S-Pointer 应用。 详情见 Appendix D。

由于 $\mathcal{C}$ 通常涉及到无限多的约束， 这个定理特别有用：它告诉我们由 $\mathcal{C}$ 引发的完整约束集合可以通过自动机 $Q$ 的有限编码来实现。 对约束闭包的进一步操作，如有效的最小化，可以在 $Q$ 上进行。通过限制与 ${^#{Start}}$ 和 ${^#{End}}$ 的转换，使用相同的算法 消去类型变量，生成所需的约束简化。

推理的整体复杂性

用于执行约束集简化类型方案构造的饱和算法， 在最坏情况下，是关于简化子类型约束数量的三次方。由于一些著名的指针分析方法也具有三次方复杂度（如 Andersen [4]）， 因此很自然地会怀疑 Retypd 的“无需指向”分析是否真的比基于指向分析数据的类型推理系统提供优势。

为了理解 Retypd 的效率所在，首先考虑 $O(n^3)$ 中的 $n$。 Retypd 的核心饱和算法在子类型约束的数量上是三次方的；由于机器代码指令的简单性，每条指令大约会产生一个子类型约束。 此外，Retypd 在每个独立的过程中应用约束简化以消除该过程局部的类型变量， 从而得到只涉及过程形参、全局变量和类型常量的约束集。在实践中，这些简化的约束集很小。

由于每个过程的约束集是独立简化的，因此三次方的 $n^3$ 因子由最大过程大小控制，而不是整个二进制文件的大小。 相比之下，像 Andersen 这样的源代码指向分析通常与指针变量的总数呈三次方，并且根据用于上下文敏感性的调用字符串深度呈

算法细节

约束简化算法（Appendix D）

基础符号

• $\amalg$ 表示集合的不交并。表示某个集合可以分割为不同的组成部分。
  • $\mathcal{V} = \mathcal{V}_i \amalg \mathcal{V}_u$ 表示类型变量集合被分割为interesting和uninteresting两部分。
• 一个证明是elementary的，如果证明的结论的子类型关系里没有uninteresting的变量，且证明过程中，uninteresting变量都只在内部。
  • $\mathcal{C} {;\vdash;}^{\mathcal{V}i}\text{elem} X.u {;\sqsubseteq;} Y.v$ 表示约束集合 $\mathcal{C}$ 上能够推理出这样一个子类型约束。其中类型变量都定义在 ${\mathcal{V}_i}$ 上，并且这样的关系是elementary的。

自动机

对应关系：

• 一个类型（sketch）就是一个有限状态自动机。
  • 本来用树就够了，但是递归类型会导致无限长的树。根据子树的有限性，用自动机处理递归的情况。典型的例子是复杂的递归结构体类型。
• 下推自动机工作的过程就是我们类型推理的过程
  • 当前状态表示基础的类型变量。
  • 栈状态表示标签，比如.load，field访问
  • 自动机配置：状态+栈状态。表示一个派生变量。
  • 状态转换规则：子类型关系。
    • 比如，随便写一个规则 $a.\sigma\mathsf{N@k} \sqsubseteq b.load$ 表示可以从状态为 $a$ 栈内容为 $\sigma\mathsf{N@k}$ 的配置转换到 状态为 $b$ 栈内容为 $load$ 的配置。
  • 可达性：派生的子类型关系。
    • 然后，如果 $b.load$ 又是 $c$ 的子类型，两个规则合起来，在自动机上，状态 $a.\sigma\mathsf{N@k}$ 到 $c$ 也是可达的（走了两步）。因此也具有子类型关系。 $a.\sigma\mathsf{N@k} \sqsubseteq c$。

Transducer 与其构建

• Transducer可以表示下推自动机的所有的推断关系！任意两个dtv字符串之间的子类型关系！
• Transducer和类型推断的对应关系。

重要概念：

• $\mathcal{P}_\mathcal{C}$ 表示我们这里构建的pushdown system。包含三部分 $(\widetilde{\mathcal{V}}, \widetilde{\Sigma}, \Delta)$

  • 状态集合： $\widetilde{\mathcal{V}} = \left(\mathsf{lhs}(\mathcal{V}_i) \amalg \mathsf{rhs}(\mathcal{V}_i) \amalg \mathcal{V}_u\right) \times { \oplus, \ominus } \cup { {^#{Start}}, {^#{End}} }$
    • 额外增加的两个特殊状态 start 和 end
    • 带有variance标签的状态，包括三部分
      • 带有L或R标签的interesting变量
      • uninteresting变量
  • 栈字符集： $\widetilde{\Sigma} = \Sigma \cup { v^\oplus | v \in \mathcal{V}_i } \cup { v^\ominus | v \in \mathcal{V}_i }$
    • 包含普通的field label
    • 带有variance标记的有趣变量。TODO这表示什么意思
  • 转换规则包括四部分 $\Delta = \Delta_\mathcal{C} \amalg \Delta_\mathsf{ptr} \amalg \Delta_\mathsf{start} \amalg \Delta_\mathsf{end}$
    • $\Delta_\mathcal{C}$ 现有的规则，经过rule函数转换后的结果
    • $\Delta_\mathsf{ptr}$ PTR规则，经过rule函数转换后的结果
    • $\Delta_\mathsf{start} = \left{\langle {{^#Start}}; {v^\oplus} \rangle \hookrightarrow \langle {v^\oplus_\mathsf{L}}; {\varepsilon} \rangle~|v \in \mathcal{V}i \right} \cup \left{\langle {{^#Start}}; {v^\ominus} \rangle \hookrightarrow \langle {v^\ominus\mathsf{L}}; {\varepsilon} \rangle|~v \in \mathcal{V}_i \right}$
      • 表示start状态可以把栈上的唯一变量标签转换为当前状态，栈为空
    • $\Delta_\mathsf{end} = \left{\langle {v^\oplus_\mathsf{R}}; {\varepsilon} \rangle \hookrightarrow \langle {{^#End}}; {v^\oplus} \rangle~|v \in \mathcal{V}i \right} \cup \left{\langle {v^\ominus\mathsf{R}}; {\varepsilon} \rangle \hookrightarrow \langle {{^#End}}; {v^\ominus} \rangle|~v \in \mathcal{V}_i \right}$
      • 表示当前状态为某个变量，栈为空的时候，可以转换到End状态，把变量放到标签。

• $\mathsf{Deriv}{\mathcal{P_C}}$ 表示 $\mathcal{P}\mathcal{C}$ 上派生得到的约束

• $\mathsf{Deriv}{\mathcal{P_C}}' = \left{ (X.u, Y.v) | (X^{\langle u \rangle}u, Y^{\langle v \rangle} v)\in \mathsf{Deriv}{\mathcal{P_C}}\right}$

  • 表示 $\mathcal{P}_\mathcal{C}$ 上删去variance标签得到的约束。

• rule辅助函数，对普通的规则，生成我们内部使用的，带variance标签的规则形式

  • $\mathsf{rule}^\oplus(p.u \sqsubseteq q.v) = \langle {\mathsf{lhs}(p)^{\langle u \rangle}}; {u} \rangle \hookrightarrow \langle {\mathsf{rhs}(q)^{\langle v \rangle}}; {v} \rangle \$
    • 首先观察到分别给左边和后边的有趣的基本类型变量，通过lhs和rhs函数带上了L/R标记
    • 其次将field label的variance标签标记到了类型变量上
  • $\mathsf{rule}^\ominus(p.u \sqsubseteq q.v) = \langle {\mathsf{lhs}(p)^{\ominus \cdot \langle u \rangle}}; {u} \rangle \hookrightarrow \langle {\mathsf{rhs}(q)^{\ominus \cdot \langle v \rangle}}; {v} \rangle \$
    • 这里的点运算符就是variance的叠加运算。
    • TODO：这里的规则有什么实际的含义吗？
  • $\mathsf{rules}(c) = { \mathsf{rule}^\oplus(c),~ \mathsf{rule}^\ominus(c)}$
    • 表示对每个约束生成两种类型的约束，带有不同的variance标记。

• 状态上的variance标签的作用：控制状态上的 ${ \oplus, \ominus }$ 上标用于追踪栈状态的当前variance，这使得我们能够区分在协变和逆变位置使用公理的情况。

• 标签 操作 lhs 和 rhs 的作用：用于防止推导中使用来自 $\mathcal{V}i$ 的变量，防止 $\mathcal{P}\mathcal{C}$ 接受代表非基本证明的推导。

  • 例如，我们写一个递归的无限约束 $var.load \sqsubseteq var$，推导为 $var.load.load \sqsubseteq var.load \sqsubseteq var$ ，在增加标签之后就变成了 $var_{L}.load \sqsubseteq var_{R}$ 从而不会被递归推导。

基于Transducer的约束简化算法包含四个步骤：

• 构建初始图
  • 生成的约束可以直接看作PDS，这里的初始图表示未化简的transducer。
• Saturation。
• Tarjan's PathExpression 算法
• 转换回约束

Saturation算法

实际算法直接构建对应的，在边上标记有push/pop序列的自动机，即Transducer。然后在上面执行saturation算法。

1. 基于约束集合构建初始图。子类型关系增加标记为1的边。对标签增加和减少的关系，增加对应push/pop的边。
   1. 规则左边存在的变量，标记pop边，右边的变量标记push边。
   2. 状态标记代表剩余的可读字符串，所以push之后反而变少，pop反而变多。
2. 运行Saturation算法，
   1. 维护Reaching Set集合 $R(x)$
      1. 初始的时候，遍历所有边，如果存在一个 push l 的边从 x 到 y 的边，则 $R(y) \leftarrow R(y) \cup {(l,x)}$ 从 x 节点 push l 可以来到 y 。即，只关注push边。
      2. 循环开始时，假如有子类型关系边 $(x, y, 1)$ ，则 $R(y) \leftarrow R(y) \cup R(x)$ 父类型更新子类型的可达关系。
   2. （循环内）Saturation规则：将 push α -> 1 -> pop a 这种边序列增加shortcut边。即，如果存在边 $(x, y, pop;l)$ 且 x 的到达集合 $R(x)$ 内有一个对应标签的到达关系 $(l,z)$ 则给增加子类型关系边 $(z, y, 1)$。
   3. 同时考虑S-Pointer规则：如果有一个 $(.store, z) \in R(x)$，想象边从 z 到 x，上面标记push store。此时找到x的逆 variance 节点 $x^-$，然后给 $R(x^-)$ 增加 $(.load, z)$
      1. 直接应用： $(.load,;x.store) \in R(\overline{x})$ 不是最典型的例子。往往会结合之前新增的子类型边。
      2. 可以想象 $x$ 到 $x^-$ 额外增加了pop store和push load边。
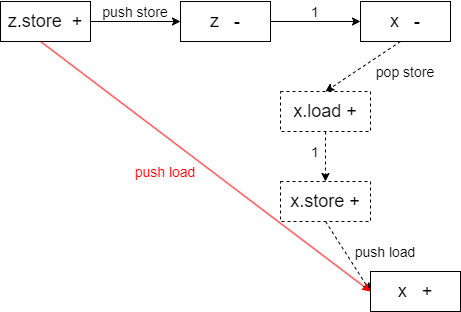
      3. 应用时最好 $\overline{x}$ 也存在在图上。

实际实现时，saturation算法被包含在Transducer的构建中。Transducer的构建在两个地方发挥作用：

• 约束的简化。
• 给sketch标记lattice元素时用来查询。

Tarjan’s path-expression algorithm 来自论文 《Fast Algorithms for Solving Path Problems》（see also this Github repo）。 在一个有向图中，求解一个源点到其他任意点的可能的路径构成的正则表达式。

在Saturation算法后，首先找到感兴趣的变量集合 $\mathcal{\epsilon}$ 然后找出所有开始并结束于 $\mathcal{\epsilon}$ 但是不经过 $\mathcal{\epsilon}$ 的路径表达式。然后和 $(recall;_)^(forget ;_)^$ 求交集（recall就是pop，forget就是push）。正则表达式也可以看作自动机，因此这里得到了一个新的自动机。

将自动机翻译为一系列子类型约束：首先将源点和目的点的基础类型变量，作为子类型关系变量的两侧。如果路径上遇到了forget标记，则在右侧增加label。遇到了recall，对应的label增加到左侧。如果存在通配关系，引入新的类型变量，表示为递归的约束。

将Transducer转换回约束（D.3 TypeScheme） 这里的算法D.3并不是直接被用。而是主要反映一个性质。上述 transducer 在构建时，我们理解为有一个隐藏的栈，会从状态push进去。这里仅仅是构建了一个完全对应的PDS，把这个栈显式地表示出来。

算法具体实现的时候，则是在前一步就找出从有趣变量到有趣变量的路径，然后直接把路径写成约束。

性质：最终得到的自动机Q有以下性质：

• 将 pop l 看作读取输入 l，push l 看作写出字符 l，1 看作空转换（ε）。则这个Transducer描述了PDS所有可能的派生关系，即所有可能的子类型关系。
• 如果在Q下，字符 Xu 能转换为 Yv，当且仅当X和Y是感兴趣变量，且存在一个基础的派生关系 $\mathcal{C} \vdash X.u \sqsubseteq Y.v$ 。

Sketches 构成的格

• sketch
  • 定义1：sketch是一个带有标记的regular tree。
  • 定义2：sketch可以被看作两个函数
    • 前缀闭合的语言： $\mathcal{L}(S) \subseteq \Sigma^*$
    • 从语言上的单词映射到lattice标记的函数 $\nu : S \to \Lambda$ ，例如 $\nu_S(w)$。
  • 定义3：通过折叠sketch子树，sketch可以表示为一个有限状态自动机，每个状态标注了一个lattice元素 $\Lambda$ 。
    • 这个自动机的每个状态都是接受态。因为语言是前缀闭合的。
  • sketch的格结构。偏序关系写作 $X \trianglelefteq Y$
    • 为sketch的树结构定义了 $\sqcup$ 和 $\sqcap$ 运算：在语言上分别是交和并。对应节点不变，或者根据variance在节点标记的格上做交或者并。

一个在变量集合V上的约束集合C的解，是一个变量到sketch的映射，满足：

• 如果是类型常量，则路径为空，lattice标记为常量
• 如果约束能推出 $X.v$ 存在，则v属于语言 $v \in \mathcal{L}(X)$
• 如果有子类型关系 $\mathcal{C} \vdash X.u \sqsubseteq Y.v$
  • 对应的节点上的lattice标记也有偏序关系
  • 对应的子树之间有sketch的偏序关系 $u^{-1} S_X \trianglelefteq v^{-1} S_Y$

sketch 和约束的对应关系很好。任何约束集合都能被一个sketch表示，只要没有证明出lattice标记上不可能的关系。

从约束构建sketches (E.1 InferShapes)

将子类型关系理解为等价关系。

1. 为每个变量，以及前缀隐含的变量存在，创建节点。
2. 构建图，边上标记field label的增加关系。
3. 划分等价关系：
   1. 如果有子类型关系，则属于一个等价类。
      1. 如果因为子类型关系在没有函数调用时是结构化的，即形状上一致，父子类型可拥有的field label一致，因此这里的父子关系划分的等价类内部，只要有一个变量能有某个label，则类内每个变量都能有这个label。
   2. 等价类内两个变量，访问相同的标签得到的变量，（有子类型关系）也在同一个等价类内。
      1. 这个地方有点像Steensgaard的线性指针分析算法。
   3. 等价类内两个变量，一个访问load标签，一个访问store标签，得到的新变量也属于同一个等价类。
4. 计算每个等价类的形状，就是等价类内每个变量的sketch的形状。

算法中实际实现时使用的步骤

1. Substitute

标记lattice元素 (F.2 Solve)

具体sketch上每个节点标什么lattice元素，借助了前面的transducer。关注所有的类型常量，然后看这个类型常量和哪些dtv有子类型关系，有则更新对应的lattice标记。根据子类型或父类型，取交或者并。

Tarjan Path Expression

基础符号

• $\epsilon(P(a,b))$ 从源点a到目标点b的路径表达式P(a,b)，所表达的所有路径的集合。
• $\Lambda$ 表示空路径，源点和目的点为同一点时，为空路径。

定义

Q&A

Q1. 为什么实现的时候，那边先infer shapes然后才简化约束？那能不能直接不简化约束了，既然我本来就想要内部的变量

确实不应该这样？简化约束应当是最早的一步，然后才是type scheme。但是这并不代表简化约束是没有意义的。因为如果其他地方如果调用了这边的函数，会实例化约束。简化了还是有好处的。

从我的其他角度：

• 先infer shapes可以获取到小的内部变量的类型，不然后面这些变量被简化没了。
• sketches可以作为函数的简化版约束，用在增量运算。关联Q3

Q2. 为什么算法要后序遍历SCC？起到什么作用？

TODO

Q3. 给定一个SCC内所有函数的已经简化完的约束。开始分析另一个调用了已分析函数的SCC，是否会对之前函数的分析结果产生影响？？

直观上看，函数就是函数本身，type schemes也就是一个函数到约束集合的映射，所以外部调用不会对函数类型有影响。细化到最具体的类型是后面考虑的事情。

如何证明？类型从形状和lattice两方面考虑。类型关系在函数调用的时候允许丢失一些能力（non-structural subtyping）。

Q4. 为什么只有函数调用的时候是non-structural subtyping?

可能一般以函数为单位做抽象？一般不会出现：函数内部一小块代码突然被看作更泛化的代码。

Q5. 如何将Sketch转换为普通类型？

从根节点出发，为所有可达路径构建path expression。？

Q6. 全局变量怎么处理？

1. 全局变量被认为是参数和返回值的拓展？在分析时作为一个interesting的变量，从而在简化约束得到type scheme的时候，能够得到它和其他类型变量之间的关系？如果其他函数也用了同样的全局变量，就可以对接上。
2. 全局变量可以看作一个无参函数？函数的type scheme是最简化的约束，假设存在任何调用者，也不因caller的调用而变化。这个角度考虑，如果看作一个无参函数，任何全局变量的类型都是一个无约束的自由类型变量。真正发挥作用的时候，仅仅是后面的附录G里面，根据使用细化类型的时候才真正产生类型。这个是不是就是retypd代码里的top down propagation？TODO
   1. 比如存在全局变量g，以及getter函数get_g和setter函数set_g。简化约束过程中，不推断G的类型。最后结束时根据使用会给G赋值一个最精确的类型。如果使用是通过get_g和set_g，则get_g因为使用获得的类型，能否从g顺着传播到set_g？

Q7. 约束的实例化是怎么做的？

• 在简化约束，求每个函数的type scheme时：
  • 如果涉及的函数调用在SCC外，则根据调用点的不同，总是创建额外的实例。例如identity函数，函数内调用多次是不同的类型。
  • 如果涉及的函数在SCC内。则不复制任何实例。TODO是这样吗？调研一下summary based analysis是如何处理递归和调用环的情况的。

另外，这说明提取约束时需要显式体现函数调用。可能可以为每个函数调用的约束增加一个调用地址标识。

Q8. 为什么要标记L和R？为什么构图时仅对左边的增加forget边，右边的变量仅增加recall边？能否证明，不标记L和R，仅仅限制路径探索不能再经过interesting的变量，即可得到相同的约束？如果不能，则得到的约束是否能用？

区分L/R以及仅对左边的增加forget边，右边的变量仅增加recall边，可以使得我们关注的变量不会存在于推导树内部。

推理关系和 proof tree 之间有对应关系。区分L和R的区别在于是否把L的变量当R的变量，从而递归推进了子类型关系。回忆elementary proof的定义，能否保证得到的约束关系的推导树，都没有感兴趣的变量在函数内部？

能否给出一个例子，使得某个saturation推导使得感兴趣的变量在推导树中间。

为了给出这样一个例子，首先回忆，为什么要简化类型约束。关键在于，是否任何原约束集合能推导出的关系，我们给出的简化的约束集合也能推导出来？

没有任何field label的F.in不能出现在该函数的子类型关系的子类型一方。同样，对应的F.out不能出现在子类型关系的父类型一方。

另外，如果一个变量仅出现在子类型关系左边（contra-variant时仅出现在右边）。不会出现反过来的情况，因此即使加上了这样的边也不会被用到。定理：如果有临时变量t，仅出现在子类型关系左边，证明不会有额外的边指向t，因此即使有边从t指向end，也不会被用到。证明：有边指向t有两种情况。第一种：构建图的时候有边指向。这种情况需要t在子类型关系右边，所以不成立。第二种，saturation时增加了边指向。根据saturation规则，仅有某个节点已经被某个pop边指向的时候，这个节点才会可能获得新增的1边。因为t没有其他边指向它，所以不成立。

Q9. 单个SCC内如何处理多态的类型关系？以及non-structural subtyping?

可以假设，能形成SCC的变量，不太可能有多态的类型关系，所以，就按照非多态的角度考虑？

TODO？这一块和full-context-sensitive的分析之间有点关系？

Q10. 为什么算法，在单个函数内关于指令是指令数的三次方的复杂度？

我们关注那个SCC的循环：生成约束的低于三次方。然后是对于每函数，这里还不是指令，不太算一个N。内部transducer函数构图，saturate，pathexpr算法。文章说saturate是主要的复杂度来源。

其实这里SCC构图之后，对每个普通的函数，已经可以做一些简单的优化了？比如一个base var没有其他的节点，然后仅有一个successor和predecessor，则可以消除。怎么有点像基本块的。

或者我可以把所有感兴趣的变量都区分L/R，先saturate一次，然后每次分析把图复制一份，merge其他的非感兴趣的图。

Q11. 函数内的类型分析算法是怎么做的？

首先，假如你已经有了被调函数的type schemes，type lattice，而且所有变量都是需要的，不需要简化。那么可以构建图，然后假设完全是non-structural subtyping，直接推导sketches。为了标记lattice，则需要构建transducer推导然后标记相关元素。

图算法基础

回顾之前的算法，我们先构建transducer图表示所有可能的子类型关系，然后饱和算法，再与productive语言相交。然后我们选择一系列感兴趣的变量，计算对应的路径表达式，然后再转换回约束。

为了将带有标记的图转换回约束，有两个相关的算法：

1. 将有限状态自动机转换为正则表达式的算法。 我们构建图的时候其实是有起始态和结束态的。把它看作一个自动机，然后即可求解出对应的正则表达式。
   1. 对每个结束状态，从它开始，利用一系列规则归纳，归纳过程中允许边上直接标记为正则表达式，最后起始态和结束态会相邻。此时删除其他状态，并总结出对应的正则表达式。
   2. 最后将得到的多个正则表达式并起来。得到最终的表达式。
2. （Tarjan's path expression算法）给定有向图，和图上的某个源点，求出源点到图上任意一个其他点之间的可达路径，所构成的表达式。
3. 两个算法之间的关联：path expression算法会构建path sequence，缓存了子图的结果。而上面的表达式算法则没有这样做，因此path expression算法效率更高一些。（TODO 对吗？）

Tarjan's path expression算法

• "Fast Algorithms for Solving Path Problems"
• "A Unified Approach to Path Problems"

定义： 给定有向图 $G=(V, E)$ ，对于单源点 s 的路径表达式（path expression）问题是，对于任何顶点v，求解出一个无歧义的路径表达式 $P(s,v)$ 使得 它所表达的路径 $\sigma(P(s,v))$ 包含了所有的从s到v的路径。

注：

• 这里指的表达式就是由路径构成的正则表达式，包括$\cup$, $*$, $;\cdot;$(连接) 等特殊符号。
• 该问题还存在变种：single-sink，all-pairs

路径序列（Path Sequence）： 一个有向图G的路径序列是一个序列 $(P_1,v_1,w_1), (P_2,v_2,w_2),...,(P_l,v_l,w_l)$ ，满足以下条件：

1. 对于 $1 \le i \le l$ ， $P_l$ 是一个无歧义的路径表达式，具有类型 $(v_i, w_i)$ (即该表达式表示从 $v_i$ 到 $w_i$ 的路径)
2. （空路径）对于 $1 \le i \le l$ ，如果 $v_i = w_i$，则空路径 $\Lambda \in \sigma(P_i)$
3. （非空路径）对于任何非空的路径p，存在一个唯一的下标序列 $1 \le i_1 \le i_2 \le ... \le i_k \le l$ 并且存在一个唯一的p的划分（不会划分出非空序列） $p=p_1,p_2,...,p_k$ 使得 $p_j \in \sigma(P_{i_j})$ 对于 $1 \le j \le k$。

如何理解非空路径条件？ 图可以被分区为 $l$ 部分，且每个分区都按顺序有个编号。然后每条路径都可以被这些部分切分，但是可能不经过部分分区。这里经过了k个分区，编号依次是 $i_1,...,i_k$。让 $j$ 从1遍历到 $k$ ，每个分区内的路径 $p_j$ 是属于对应分区的路径表达式能够表达的所有路径集合 $\sigma(P_{i_j})$。

如何理解路径序列？ 任何图上的路径需要被分解为路径序列。

• 比如我们可以构造一个路径序列，从图上任意点到任意点，则每个路径能直接找到对应。此时路径序列的顺序不重要。
• 对于有向无环图，每个边可以单独成为一个路径序列，因为这个边是连接这两个节点的唯一必经路径。每个路径可以直接分解为每条边，然后对应到路径序列中。。
• 对于强连通分量这种复杂情况，实在不行我们可以为里面任意两个点构建路径序列。如果有路径经过了强连通分量内部，如果能直接找到对应，则此时分量内部路径序列的顺序不重要。

Solve算法：给定一个路径序列，我们可以使用下面的传播算法解决单源点的路径表达式问题。

• 初始化：设置 $P(s,s) = \Lambda$ ，同时对每个不为s的顶点，初始化 $P(s,v) = \emptyset$
• 循环：让i从1到 $l$ （有 $l$ 个顶点）
  • 如果 路径序列 $(P_i,v_i,w_i)$ 中的 $v_i = w_i$ ， $P(s, v_i):= [P(s,v_i);\cdot;P_i]$
  • 如果 $v_i \ne w_i$ ，$P(s,w_i) = [P(s,w_i)\cup[P(s,v_i);\cdot;P_i]]$

（这个算法基本上就是把路径连接起来。另外意味着我们需要按拓扑排序给节点一个编号）

路径表达式简化算法（方括号）：

• 如果路径表达式 R 具有形式 $R_1 \cup R_2$ 则，
  • 如果任意一边为空集合，则直接简化为另外一边
• 如果路径表达式具有形式 $R_1;\cdot;R_2$ 则
  • 如果任意一边是空集，则直接返回空集
  • 如果任意一边是空路径，则直接简化为另外一边
• 如果路径表达式具有形式 $R_1^*$
  • 如果 $R_1$ 是空集或者空路径，则直接返回空路径
• 否则原样返回

使用Solve函数解决路径问题

• 对于单源点路径表达式问题（single-source path expression），我们构建Path Sequence然后调用Solve一次
• 对于所有节点对的路径表达式问题（all-pairs path expression），我们构建Path Sequence然后把每个点作为源点，调用Solve。
• 对于单目的点的路径表达式问题（single-sink path expression），我们构建一个边都是反向的图，然后转换为单源点的路径表达式问题。

Eliminate算法： 我们可以对任意的图构建路径序列。

• 初始化：
  • $P(v, w):=\varnothing$ 任意两个顶点间都初始化为空集合
  • 然后对每个边 $e \in E$ ， 让路径表达式包含当前边 $P(h(e), t(e)):=[P(h(e), t(e)) \cup e]$
• 求解的主循环：
  • 让v遍历每个节点序号1到n
    • $P(v, v)=\left[P(\nu, v)^*\right]$
    • 遍历每个 $u \gt v$ ，如果 $P(u, v) \neq \varnothing$
      • $P(u, v):=[P(u, v) \cdot P(v, v)]$
      • 遍历每个 $w \gt v$ ，如果 $P(v, w) \neq \varnothing$
        • $P(u, w):=[P(u, w) \cup[P(u, v) \cdot P(v, w)]]$

比如，如果一个有向无环图，按照拓扑排序编号，则 $u \gt v$ 时， $P(u, v)$ 必然为空，导致该算法无法进入循环，什么也做不了。但是实际上，初始化过程中，就已经完成了path sequence的构建了。因为有向无环图的路径序列就是每个边单独构成的序列。

Eliminate结果的顺序：Eliminate算法计算得到的结果，需要按照正确的顺序排列才能形成路径序列：

Theorem 4. Let $P(u, w)$ for $u, w \in V$ be the path expressions computed by ELIMINATE. Then the following sequence is a path sequence: the elements of ${(P(u, w), u, w) \mid P(u, w) \notin{\varnothing, \Lambda} ; and ; u \leq w}$ in increasing order on $u$, followed by the elements of ${(P(u, w), u, w) \mid P(u, w)=\varnothing ; and ; u>w}$ in decreasing order on $u$.

问题的分解： 为了提升Eliminate算法的效率，有两种方法，他们都对图进行分解。首先可以将图按强连通分量SCC分解。

有向无环图的路径序列： 首先将节点按照拓扑排序编号，可以直接得到集合 ${(e, h(e),t(e))|e\in E}$ 将这个集合中的点按照 $h(e)$ 升序排序，可以直接得到路径序列。

拓展到任意有向图： 对于有向图G，首先将图中的强连通分离凝结成单个点表示，则可以得到有向无环图，这些节点 $G_1,G_2,...,G_k$ 表示图G中的一个子图，编号按照拓扑排序。假设这些子图的路径表达式是 $X_1,...,X_k$ ，设 $Y_l$ 是序列 ${e,h(e),t(e)|h(e) \in G_l ; and ; t(e) \notin G_l}$ 任意排序（注意到 $Y_k$ 为空）。则 $X_1,Y_1,X_2,Y_2,...,X_{k-1},Y_{k-1},X_k$是G的一个路径序列。

与其他算法的关系

Retypd与现有指针分析的关系

Steensgaard 线性时间 指针分析

相关资料：

1. DCC888 编译器静态分析课 Pointer Analysis
2. 北京大学 软件分析 熊英飞

与 Anderson 指针分析的关系

对应retypd论文中Constraint generation一节。

对于语句 q = &x，如何生成约束？有两种方式

• x是q加载后的子类型（提前假设q会被load）： 生成 x <= q.load.off0@N
• q存入值是x的子类型（提前假设q会被store）：生成 q.store.off0@N <= x

需要考虑的问题是，立刻生成这两个约束，和维护一个指针分析，根据指针分析的结果生成这些约束。这两种方式是否有区别。

• 假如提前生成了这个约束，是否会产生什么额外的影响？
  • 直观来说，额外生成的 q.load.off0@N q.store.off0@N 还能有谁指向吗？
• 如果Steensgaard指针分析能推断出指向关系，假如不产生指针分析的约束，原有类型系统是否依然能推断出来类型关系。

证明：

分每种语句考虑(TODO 证明 offset和load/store可以绑定/合并)

• 语句1：对于 x = &O1，对应 O1 <= x.load 和 x.store <= O1 我们把指向关系定义为这两个关系的组合。
• 语句2：对于 y = x (x <= y)，在retypd下有如下图结构：

在指针分析中有如下约束： pts(x) $\subseteq$ pts(y) 我们尝试证明：

• 对于任何x可能指向的对象，y也会指向它。
  • 1 已知 O1 <= x.load ，证明 O1 <= y.load：证：由 x.load <= y.load 显然 O1 <= x.load <= y.load
  • 2 已知 x.store <= O1 ，证明 y.store <= O1：证：由y.store <= x.store 显然 y.store <= x.store <= O1

能否证明充要条件？如果存在 O1 <= x.load 和 x.store <= O1 则必然在Anderson指针分析中有 O1 $\in$ pts(x)

则我们可以证明，retypd是一种基于anderson指针分析的类型推断算法。

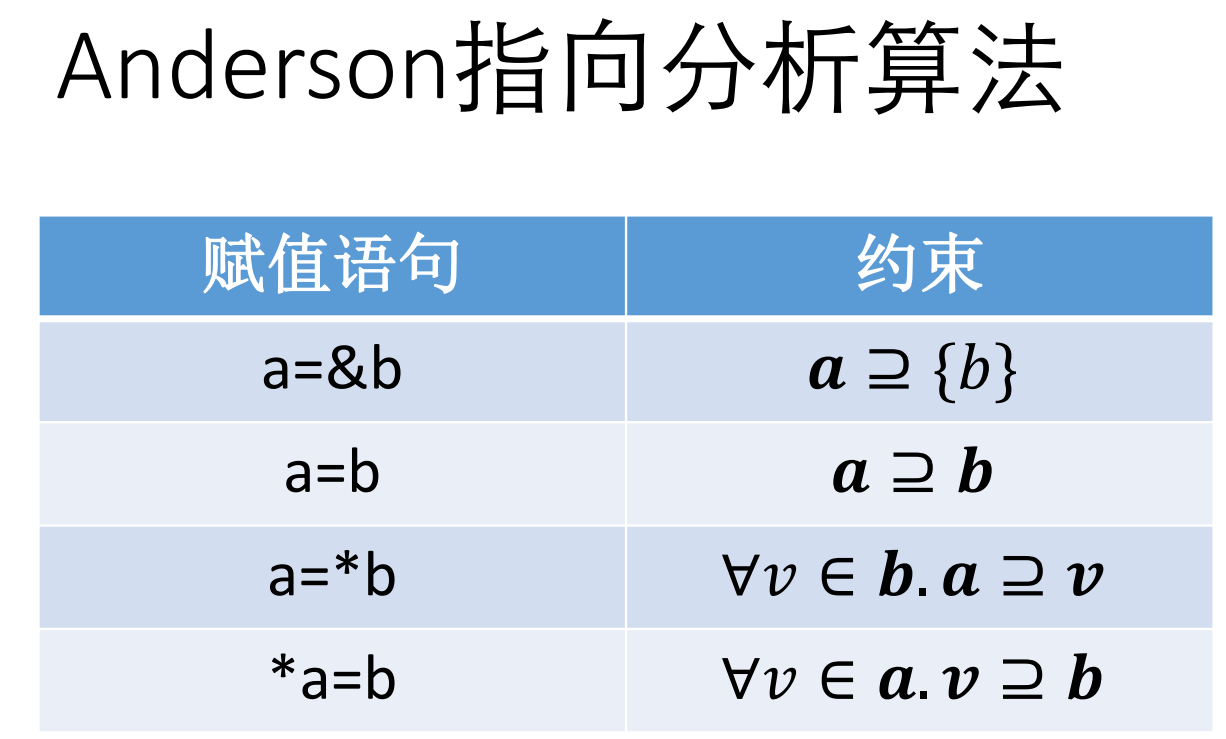
语句3：对于a = *b，有 b.load <= a

• 方式1 提前生成约束： 由归纳法，如果之前的其他语句都能够维持和指针分析等效的分析关系，当前语句依然能维持关系，则关系继续维持。
  • 提前生成约束会额外生成约束： 对于任何 O $\in$ pts(b) 有 b.store <= O 似乎影响不大？
• 方式2 根据指针分析生成约束：对于任何 v $\in$ pts(b) ，生成/之前有 v <= b.load。因此有 v <= b.load <= a。对应 v $\subseteq$ a

语句4：对于*a = b，有 b <= a.store

• 根据指针分析生成约束：对于任何 v $\in$ pts(a) ，之前有 a.store <= v。所以有 b <= a.store <= v。对应 b $\subseteq$ v

• saturation算法和Anderson指针分析算法求解时的异同。

• retypd如果没有区分指针的load和store，是否依然和anderson指针分析一致？

  • 不行，明显上面的证明是和load和store性质有很大关系的。

问题：offset和load/store可以绑定/合并

证明：首先.in 和.out只能在最外层。因此没有什么能够介入load/store中间。其次，每次load和store必然有offset和size。我们讨论某个变量的load和store的时候，本质上在讨论所有可能的offset和size之间的关系/对应的结构体类型。

结构体域敏感的指针分析

《Efficient Field-Sensitive Pointer Analysis for C》中提出了几种新的操作

实现 - 约束生成

基本运算

根据指令的依赖关系，自底向上处理指令，插入到指令到约束集合的集合。生成约束变量。

• 指针相关
  • 存地址运算：由上面的证明，直接假设它之后会被load/store，生成两条约束。
• 变量赋值/数据流传递：对应子类型关系。
• 加法和减法约束
  • 函数内是双向数据流分析，但是要和Summary-based analysis结合，无法求解的约束存到summary里尝试化简。

加减法约束

加减法约束的计算问题，其实是一个双向数据流分析问题。对应关系如下：

• 数据流流动关系，即SSA上的def-use关系，对应约束生成时的子类型关系，都是一种边。
• 指针类型关于子类型关系双向传递，子类型关系可以看作是数据流分析的边，加减法看作带有运算的基本块。然后基于worklist算法，递归应用约束，直到迭代到不动点。。
• 子类型关系。

因为本来就有基于类型的alias analysis。所以涉及指针的时候，类型分析和指针分析和别名分析真的有联系。

• 指针分析是别名分析的更精确版本。别名分析可以看作指针分析的应用。
• 类型分析需要随着指针指向去传播。
• 类型分析涉及指针时，不需要考虑流敏感性，上下文敏感性。

其他

SSA的静态分析和传统静态分析

• SSA的静态分析是在 SSA Edge ，即def-use chain上进行，遇到Phi指令merge结果。。
• 传统静态分析在CFG上进行，遇到控制流合并时merge结果。

静态分析之间的分层依赖

静态分析直接可能有依赖关系。比如指针和数字类型区分就被retypd类型恢复依赖，retypd进一步恢复指针的具体类型。

静态分析之间，是依赖关系还是更复杂的的关系。在于是否上层依赖的分析结果会反哺下层分析的结果。比如这里retypd如果恢复了更详细的具体类型，比如两个指针指向的结构体成员之间的复杂关系，那么这两个就有关系。。

问题：基于Steensgaard的线性时间指针分析算法的合并存储图，和retypd的sketches 等价图分析指针和数字类型，达到的精度是否相同？

答：应该是相同的。retypd的等价图构建后就等价是Steensgaard的存储关系图。

但是在跨函数分析框架下，这些具体分析都是一样地需要专门看待。。

Datalog

基于Datalog描述程序分析的优点是开发迅速。

• Souffie使用了Futamura projections技术将datalog转C++代码

现有工具/资料

• 综述，介绍datalog：Datalog and Recursive Query Processing

基于Datalog的LLVM分析

• Vandal

基于Datalog的反编译（相关的工作）

• webassembly decompilation based on datalog
• elipmoc/gigahorse
• ddisasm

博客

• Dimension Shift! 一起来学Datalog吧！

将LLVM IR导出为Datalog规则

Datalog挺像数据库的。Souffle的语法也拓展了很多特性，使得导出的写法不止一种。

• VandalIR，基于python的llvmlite模块，直接解析IR字符串。
  • 导出IR时给每个函数和基本块有一个ID。
  • 指令还有一个virtual register，即指令%xx = ...最左边的部分。LLVM中负责打印IR的相关的源码在llvm\lib\IR\AsmWriter.cpp，可以看到，有Name的会打印Name，没有Name的打印编号Slot是由WriterCtx.Machine负责的。因此总体上还是按照LLVM的规范，依次给没有Name的Value按顺序赋序号。
  • 指令没有新的方式。

几个需要考虑的设计选择：

• 如何给每个函数、基本块、指令确定一个ID？
  • （最后选了）使用valueID，给每个Value一个ID，包括指令，函数参数，基本块，函数。类似的，给每个类型一个ID，用类型的字符串表示做去重。
    • 使用AssemblyAnnotationWriter，给IR里面的指令用注释标出来编号。
  • 函数名-基本块编号-指令编号：因为根据这里，基本块在函数里的顺序是不会边的
  • 使用函数名-基本块名-指令名
    • 导出前用一个Pass给每个没有名字的基本块，指令命名。
    • 没有名字的使用printAsOperand获取。但是这样还是有问题，对于没有返回值的指令，比如store，会打印void <badref>。这种情况可以另外单独给个ID。
  • 使用基本块地址，指令的地址：LLVM不会移动指令。但是要求得在单次运行中完成，即直接导入souffle依赖，在内存里传递facts。
• 指令的表示
  • 每个指令单独一个decl
  • 指令复用同一个decl：用id/enum表示不同的指令opcode，引用其他指令就用Pos/ID表示
    • 遇到了常量怎么办？给常量也有一个ID？

Other Notes

这里包括一些其他笔记，如C++，CMake的使用。

C++ Development

stackoverflow

1. 代码规范遵守LLVM的，https://llvm.org/docs/CodingStandards.html#do-not-use-rtti-or-exceptions 注意不要使用异常处理，用abort替代。可以使用特殊的宏辅助打印错误信息。

   if(this->globs.size() != 0) {
       std::cerr << __FILE__ << ":" << __LINE__ << ": " << "Error: Cannot add module when globals is not empty" << std::endl;
       std::abort();
   }
   

2. 最好不要在头文件里用using namespace。但是可以在函数体开头使用。 https://stackoverflow.com/questions/223021/whats-the-scope-of-the-using-declaration-in-c
3. 返回值选择object还是pointer： https://stackoverflow.com/questions/13213912/returning-an-object-or-a-pointer-in-c
4. 是否使用智能指针：https://stackoverflow.com/questions/106508/what-is-a-smart-pointer-and-when-should-i-use-one
5. 用引用还是指针：https://stackoverflow.com/questions/7058339/when-to-use-references-vs-pointers
6. 引用和指针的区别：https://stackoverflow.com/questions/57483/what-are-the-differences-between-a-pointer-variable-and-a-reference-variable

注意事项

1. 注意相关STL函数使用要带上check。
   1. vector使用back一定要检查是否是空！！！ assert(stack.size() > 0);

CMake Notes

CMake 学习资料

1. https://eliasdaler.github.io/using-cmake/
2. https://github.com/kigster/cmake-project-template 找一个模板项目作为参考

External Project

基本就是先添加ExternalProject_add，然后add_library指定IMPORTED，设置import路径。最后使用的时候额外增加一个add_dependencies关联到ExternalProject_add的target。

1. https://cmake.org/cmake/help/latest/module/ExternalProject.html
2. https://stackoverflow.com/questions/51564251/correct-way-to-use-third-party-libraries-in-cmake-project/51567322#51567322
3. https://stackoverflow.com/questions/51661637/having-cmake-build-but-not-install-an-external-project
4. https://stackoverflow.com/questions/29533159/what-is-install-dir-useful-for-in-externalproject-add-command
5. ninja报错找不到import的库的构建方法： https://stackoverflow.com/questions/50400592/using-an-externalproject-download-step-with-ninja